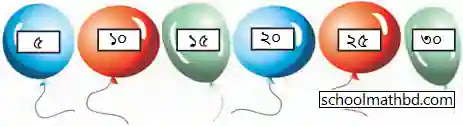Amar Ganit Class 4 – মাঠে টিফিন ভাগ করে খাই – সমতুল্য পাঠ ২১ – পাতা (১৫৯-১৬৭)
মাঠে টিফিন ভাগ করে খাই
আমি, সায়রা ও সুদীপ রোজ খেলার মাঠে যাই। প্রতিদিন খেলার
মাঠে আমরা খাবার ভাগ করে খাই। গত রবিবার মা বাড়িতে লাড্ডু তৈরি করেছে। আমার বন্ধুরা
লাড্ডু খেতে ভালোবাসে। কিন্তু কতগুলো লাড্ডু নিয়ে গেলে আমরা তিনজনে না ভেঙে সমান ভাগে
ভাগ করে খেতে পারি দেখি?
|
নিয়ে যাওয়া লাড্ডু সংখ্যা
|
৩ জনের প্রত্যেকে পাব
|
|
৩
|
১টি
|
|
৪
|
১টি, অবশিষ্ট থাকবেঃ ১টি
|
|
৫
|
১টি, অবশিষ্ট থাকবেঃ ২টি
|
|
৬
|
২টি
|
|
৯
|
৩টি
|
|
১২
|
৪টি
|
এবার দেখি কতগুলি লাড়ু নিয়ে গেলে প্রত্যেকে না ভেঙে সমান
সংখ্যক লাড়ু খেতে পারব?
|
যখন আমরা ৩ জন
|
তখন আমরা প্রত্যেকে পাবঃ
|
|
৩×১=৩
|
১টি
|
|
৩×২=৬
|
২টি
|
|
৩×৩=৯
|
৩টি
|
|
৩×৪=১২
|
৪টি
|
|
৩×৫=১৫
|
৫টি
|
তাই দেখছি যত বেশি লাড্ডু নেব তত বেশি করে প্রত্যেকে পাব। এমন সংখ্যক লাড্ডু নেব যে সংখ্যাগুলোকে ৩ দিয়ে ভাগ করা যায়।
দেখলাম লাড্ডুর সংখ্যাগুলো অর্থাৎ ৩,৬,৯,১২,১৫…..সবগুলোই
৩-কে পরপর ১,২,৩,৪,৫……. গুণ করে পাচ্ছি। ৩,৬,৯,১২,১৫…..এদের ৩-এর কী বলা হয়?
উত্তরঃ
৩,৬,৯,১২,১৫…..কে ৩-এর গুণিতক বলা হয়।
আবার,
|
যখন আমরা ৪ জন
|
তখন আমরা প্রত্যেকে পাবঃ
|
|
৪×১=৪
|
১টি
|
|
৪×২=৮
|
২টি
|
|
৪×৩=১২
|
৩টি
|
|
৪×৪=১৬
|
৪টি
|
|
৪×৫=২০
|
৫টি
|
শিখন ফলাফলঃ
শূন্য ছাড়া ৪-এর গুণিতকগুলো হলোঃ ৪,৮,১২,১৬,২০,২৪,…..
নীচের বেলুনে তুমি শূন্য ছাড়া ৫-এর ৬টি গুণিতক লিখ।
সমাধানঃ
নতুন খেলা খেলি [পাতা-১৬১]
রাজু ও রোজিনা আজ নতুন খেলা খেলবে। রাজু বাড়ির সামনের চাতালে
দাগ কেটে ১,২………১৫ পর্যন্ত পরপর লিখেছে। রাজু বাঘের মুখোশ পরেছে। আর রোজিনা পরেছে একটা
বিড়ালের মুখোশ। আমি বাড়ি থেকে ২ ঘর বাদ দিয়ে বাঘের মতো লাফিয়ে এগিয়ে যাব ও আমি যে ঘরে
যাব সেই ঘরে ▲ কার্ড রাখব।
▲ কার্ড আছে _৩_,_৬_,_৯_,_১২_,_১৫_ ঘরগুলো।
অর্থাৎ, ৩-এর গুণিতকের ঘরগুলোয় রাজু
▲ কার্ড
রেখেছে।
আবার,
আমি বাড়ি থেকে ১ ঘর বাদ দিয়ে বিড়ালের মতো লাফিয়ে এগিয়ে
যাব ও আমি যে ঘরে যাব সেই ঘরে ◼
কার্ড রাখব।
◼ কার্ড
আছে _২_,_৪_,_৬_,_৮_,_১০_,_১২_ ঘরগুলো।
অর্থাৎ, ২-এর গুণিতক ঘরগুলোয় আমি ◼ কার্ড
রেখেছি।
দেখছি, ▲ ও ◼ দুটি
কার্ডই একসঙ্গে পড়ে আছে _৬_ ও _১২_
কিন্তু কেন এমন হলো?
৬-এর ঘরে ▲ কার্ড আছে, কারণ ৬=৩×২ অর্থাৎ
৬, ৩-এর গুণিতক।
আবার, ৬-এর ঘরে ◼ কার্ড আছে, কারণ ৬=২×৩ অর্থাৎ ৬, ২-এর গুণিতক।
আবার ১২-এর ঘরে ▲ কার্ড আছে, কারণ ১২=৩×৪ অর্থাৎ ১২, ৩-এর গুণিতক।
১২-এর ঘরে ◼ কার্ড আছে, কারণ ১২=২×৬ অর্থাৎ ১২, ২-এর গুণিতক।
পেলাম, ৬, ৩-এর এবং ২-এরও গুণিতক।
১২-এর গুণিতকগুলি লিখ।
সমাধানঃ
_১২_,_২৪_,_৩৬_,_৪৮_,_৬০_,_৭২_,_৮৪_,_১০৮_,……..
নিজে করি [পাতা-১৬৩]
১) শূন্য ছাড়া ৬-এর ৮টি গুণিতক লিখি।
সমাধানঃ
_৬_, _১২_, _১৮_, _২৪_, _৩০_, _৩৬_, _৪২_, _৪৮_, _৫৪_
২) শূন্য ছাড়া ৫-এর ৮টি গুণিতক লিখি।
সমাধানঃ
_৫_, _১০_, _১৫_, _২০_, _২৫_, _৩০_, _৩৫_, _৪০_
৩) ৬ ও ৫-এর ১টি সাধারণ গুণিতক লিখি।
সমাধানঃ
৩০
৪) ৬ ও ৫-এর ৪টি সাধারণ গুণিতক লিখি।
সমাধানঃ
_৩০_, _৬০_, _৯০_, _১২০_।
হাতেকলমে [পাতা-১৬২]
হাতেকলমে ২ ও ৩-এর সাধারণ গুণিতক ও লঘিষ্ঠ সাধারণ গুণিতক
খুঁজি।
তিনটি ১৫ সেমি. লম্বা ও ৭ সেমি. চওড়া কাগজ নিলাম। প্রতিটি
কাগজে নীচের মতো ১০০টি সমান ঘর টানলাম।
প্রথম কাগজঃ
প্রথম কাগজে ১ থেকে ১০০ পর্যন্ত ছবির মতো লিখলাম।
দ্বিতীয় কাগজঃ
দ্বিতীয় কাগজে একটা ঘর বাদ দিয়ে গর্ত করলাম।
তৃতীয় কাগজঃ
তৃতীয় কাগজে দুটো ঘর বাদ দিয়ে গর্ত করলাম।
১. প্রথম কাগজের উপরে দ্বিতীয় কাগজ বসিয়ে ২-এর গুণিতকগুলো
দেখতে পাচ্ছি। অর্থাৎ ২,৪,৬,৮,…….. দেখতে পাচ্ছি।
২. প্রথম কাগজের উপর তৃতীয় কাগজ বসিয়ে ৩-এর গুণিতকগুলো
দেখতে পাচ্ছি। অর্থাৎ ৩,৬,৯,…. দেখতে পাচ্ছি।
৩. এবার প্রথম কাগজের উপরে দ্বিতীয় ও তৃতীয় কাগজ বসিয়ে
দেখতে পাচ্ছি, ৬,১২,১৮,২৪……..।
ফলাফলঃ
শূন্য ছাড়া ২-এর গুণিতকগুলোঃ _২_, _৪_, _৬_, _৮_, _১০_, _১২_, _১৪_, _১৬_, _১৮_, _১৯_, _২০_।
শূন্য ছাড়া ৩-এর গুণিতকগুলোঃ _৩_, _৬_, _৯_, _১২_, _১৫_, _১৮_, _২১_, _২৪_, _২৭_, _৩০_।
২ ও ৩-এর সাধারণ গুণিতকগুলোঃ _৬_, _১২_, _১৮_, _২৪_, _৩০_, _৩৬_, _৪২_, _৪৮_, _৫৪_।
২ ও ৩-এর লঘিষ্ঠ সাধারণ গুণিতকঃ _৬_।
খরগোশ ও ক্যাঙ্গারুর লাফানো দেখি [পাতা-১৬৫]
প্রশ্নঃ একটি ক্যাঙ্গারু ০-এর ঘর থেকে শুরু করে ৪-ঘর করে
লাফাচ্ছে এবং একটি খরগোশ ০-এর ঘর থেকে শুরু করে ৩-ঘর করে লাফাচ্ছে। এখন হিসাব করে দেখি
কাঙ্গারু ও খরগোশ উভয়েই কোন কোন ঘরে লাফিয়ে পড়ছে।
হিসাবঃ
ক্যাঙ্গারু লাফানো ঘরগুলোঃ _৪_, _৮_, _১২_, _১৬_, _২০_, _২৪_,…….
অর্থাৎ, ক্যাঙ্গারু লাফাচ্ছে ৪-এর গুণিতক ঘরে।
তাই শূন্য ছাড়া ৪-এর গুণিতকগুলোঃ _৪_, _৮_, _১২_, _১৬_, _২০_, _২৪_,…….
আবার,
খরগোশের লাফানো ঘরগুলোঃ _৩_, _৬_, _৯_, _১২_, _১৫_, _১৮_, _২১_, _২৪_,…….
অর্থাৎ, খরগোশ লাফাচ্ছে ৩-এর
গুণিতক ঘরে ।
তাই শূন্য ছাড়া ৩-এর গুণিতকগুলোঃ- _৩_, _৬_, _৯_, _১২_, _১৫_, _১৮_, _২১_, _২৪_,…….
পেলাম ৪ ও ৩-এর দুটি সাধারণ গুণিতকঃ _১২_, _২৪_,……….
বা, ৪ ও ৩-এর সাধারণ গুণিতকগুলোঃ ১২,২৪,৩৬,৪৮,৬০,৭২,৮৪,৯৬,১০৮,………..
অর্থাৎ, ৪ ও ৩-এর সাধারণ গুণিতকের সংখ্যা অসংখ্য।
এই সাধারণ গুণিতকগুলোর মধ্যে সর্বকনিষ্ট সংখ্যাঃ ১২
পেলাম, ৪ ও ৩-এর লঘিষ্ঠ সাধারণ গুণিতক ১২।
দুটি ঘরে বসাই [পাতা-১৬৭]
মিলি ও মানস দুজনে দুটি রঙিন কাগজে আলাদা আলাদা গুণিতক
তৈরি করবে। মিলি শূন্য ছাড়া ৫-এর গুণিতকগুলো তার হলুদ রঙের কাগজে লিখেছে।
৫ এর গুণিতকগুলোঃ
|
৫
|
১০
|
১৫
|
২০
|
২৫
|
|
৩০
|
৩৫
|
৪০
|
৪৫
|
৫০
|
|
৫৫
|
৬০
|
৬৫
|
৭০
|
৭৫
|
|
……………………………………
|
||||
মানস শূন্য ছাড়া ৬-এর গুণিতকগুলো তার সবুজ রঙের কাগজে লিখেছে।
৬-এর গুণিতকগুলোঃ
|
৬
|
১২
|
১৮
|
২৪
|
৩০
|
|
৩৬
|
৪২
|
৪৮
|
৫৪
|
৬০
|
|
৬৬
|
৭২
|
৭৮
|
৮৪
|
৯০
|
|
……………………………………
|
||||
এখন, মিলির গলুদ কাগজে লিখিত কিছু সংখ্যা মানসের সবুজ কাগজে
লিখিত সংখ্যার সাথে মিলে যাচ্ছে।
এবার মিলি ও মানস তাদের কাগজে লিখিত যে সকল সংখ্যাগুলো
একই সেগুলো হলোঃ ৩০,৬০,……..
অর্থাৎ, ৫ ও ৬-এর সাধারণ গুণিতকগুলো হলোঃ ৩০,৬০,……..
নিজে করি [পাতা-১৬৭]
১) নিচে প্রদত্ত ২-এর গুণিতগুলোকে ____ ও ৫-এর গুণিতগুলোকে ____ দ্বারা বেষ্টিত করি।
৪,৫,২,৭,১১,১৫,৮,২৫,১৪,১৩,১৭,২২৩৫,৩২,৩১,৩৩,২৩,২৬,৪৫,৪৪,৩৪,৬৭,৩৯,৪১,৪২,৪৩,৪৬,৪৭,৪৮,৪৯.
সমাধানঃ
৪,৫,২,৭,১১,১৫,৮,২৫,১৪,১৩,১৭,২২,৩৫,৩২,৩১,৩৩,২৩,২৬,৪৫,৪৪,৩৪,৬৭,৩৯,৪১,৪২,৪৩,৪৬,৪৭,৪৮,৪৯.
২) নীচের রেখায় বিদ্যমান শূন্য পরবর্তী সংখ্যাগুলো থেকে
২ ও ৪-এর সাধারণ গুণিতকগুলো এবং সবচেয়ে ছোট সাধারণ গুণিতক খুঁজি।
সমাধানঃ
২-এর গুণিতিকগুলোঃ ২,৪,৬,৮,১০,১২,১৪,১৬,……
৪-এর গুণিতকগুলোঃ ৪,৮,১২,১৬,……..
তাহলে, ২ও ৪-এর সাধারণ গুণিতকগুলোঃ ৪,৮,১২,১৬,……….
∵
২ ও ৪-এর সবচেয়ে ছোট সাধারন গুণিতকঃ ৪
৩) নিচের রেখাতে ০ ছাড়া ৭-এর গুণিতকগুলোতে যাই ও লিখি।
২ নং চিত্রটি দেখ।
সমাধানঃ
শূন্য ছাড়া ৭-এর গুণিতকগুলোঃ _৭_, _১৪_, _২১_, _২৮_,……………
৪) ৮ ও ৬-এর ২টি সাধারণ গুণিতক লিখি।
সমাধানঃ
৪৮, ৯৬
৫) জুলেখা, জালাম ও শিলা যথাক্রমে তার লাল, নীল ও সবুজ
গোলে যথাক্রমে ২-এর ১২টি, ৩-এর ১২টি ও ৪-এর ১২টি গুণিতক লিখল।
এখন, ২,৩, ও ৪-এর সাধারণ গুণিতকগুলো খুঁজি ও নিন্মচিত্রে
চিহ্নিত স্থানে লিখি।
সমাধানঃ
২-এর ১২টি গুণিতকঃ
২,৪,৬,৮,১০, ১২,১৪,১৬,১৮,২০,২২,২৪
৩-এর ১২টি গুণিতকঃ ৩,৬,৯,১২,১৫,১৮,২১,২৪,২৭,৩০,৩৩,৩৬
৪-এর ১২টি গুণিতকঃ ৪,৮,১২,১৬,২০,২৪,২৮,৩২,৩৬,৪০,৪৪,৪৮
∵
২,৩ ও ৪-এর সাধারণ গুণিতকগুলোঃ ১২,২৪,…… যা নিন্ম চিত্রে প্রশ্নানুসারে দেখানো হলো।
পরের পাঠঃ