দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ – Class 7 Math BD 2023 – দ্বাদশ অধ্যায় (২৩৪ ও ২৩৬ পৃষ্ঠা)

দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ

অজানা রাশির সমীকরন অধ্যায়ের এই অংশে আমরা ২৩৪ পৃষ্ঠা ও ২৩৬ পৃষ্ঠার দাঁড়িপাল্লার ভারসাম্য্য ও আদর্শ সমীকরণ বিষয়ক সমস্যার সমাধান করেছি। নিচে সমস্যার সমাধানসমূহ দেয়া হলোঃ

একক কাজ (২৩৪ পৃষ্ঠা)

দাঁড়িপাল্লার ভারসাম্যের সাহায্যে নিচের সমীকরণগুলো সমাধান করে দেখাও।

১. কোন সংখ্যার দ্বিগুণের বা দুইগুণের সাথে 5 যোগ করলে যোগফল 25 হবে?

২. দুইটি সংখ্যার যোগফল 55 এবং বড় সংখ্যাটির 5 গুণ ছোট সংখ্যাটির 6 গুণের সমান। সংখ্যা দুইটি নির্ণয় করো।

৩. গী তা, রি তা এবং মি তা র একত্রে 180 টাকা আছে। রিতার চেয়ে গী তা র 6 টাকা কম ও মি তা র 12 টাকা বেশি আছে। কার কত টাকা আছে?

সমাধানঃ

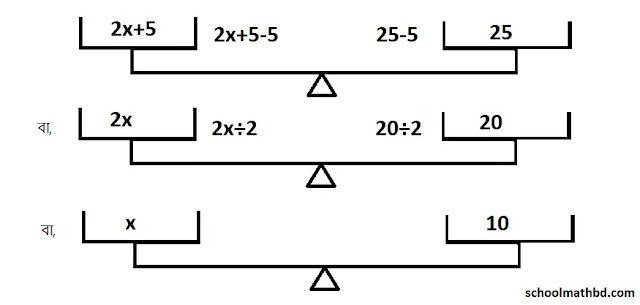
১নং এর সমাধানঃ

মনে করি, একটি সংখ্যা x

তাহলে x এর দ্বিগুনের সাথে 5 যোগ করলে হয় 2x+5

প্রশ্নমতে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় 2x+5 ও অন্য পাল্লায় 25 রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি। 

অতএব, সংখ্যাটি = 10

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

2x+5 = 25

বা, 2x+5-5 = 25-5 [উভয়পক্ষ থেকে 5 বিয়োগ করে]

বা, 2x = 20

বা, 2x÷2 = 20÷2 [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, x = 10

অতএব, সংখ্যাটি = 10

২নং এর সমাধানঃ

মনে করি, বড় সংখ্যাটি x

তাহলে, ছোট সংখ্যাটি = (55-x)

প্রশ্নমতে,

5x = 6(55-x)

তাহলে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় 5x ও অন্য পাল্লায় 6(55-x) রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি।

অতএব, বড় সংখ্যাটি = 30

এবং ছোট সংখ্যাটি = (55-30) = 25

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

5x = 6(55-x)

বা, 5x = 330-6x

বা, 5x+6x = 330

বা, 11x = 330

বা, ^11x/₁₁ = ³³⁰/₁₁ [উভয়পক্ষকে 11 দ্বারা ভাগ করে]

বা, x = 30

অতএব, বড় সংখ্যাটি = 30

এবং ছোট সংখ্যাটি = (55-30) = 25

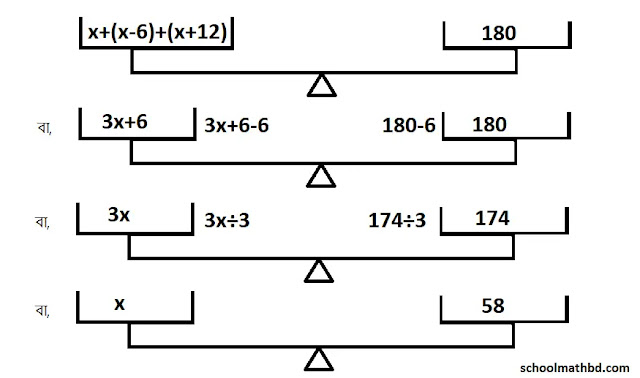
৩নং এর সমাধানঃ

মনে করি, রিতার আছে x টাকা

তাহলে, গীতার আছে x-6 টাকা এবং মিতার আছে (x+12) টাকা।

প্রশ্নমতে,

x+(x-6)+(x+12) = 180

তাহলে, দাঁড়িপাল্লার ভারসাম্য হবে এক পাল্লায় x+(x-6)+(x+12)  ও অন্য পাল্লায় 180 রাখলে এবং এই প্রক্রিয়ার সাহায্যে নিন্মোক্তভাবে আমরা x এর মান বের করি।

অতএব, রিতার আছে 58 টাকা

গীতার আছে (58-6) টাকা = 52 টাকা

মিতার আছে (58+12) টাকা = 70 টাকা।

উক্ত পদ্ধতির গাণিতিক সমাধানঃ

x+(x-6)+(x+12) = 180

বা, 3x+6 = 180

বা, 3x+6-6 = 180-6 [উভয়পক্ষ থেকে 6 বিয়োগ করে]

বা, 3x = 174

বা, ^3x/₃ = ¹⁷⁴/₃ [উভয়পক্ষকে 3 দ্বারা ভাগ করে]

বা, x = 58

অতএব, রিতার আছে 58 টাকা

গীতার আছে (58-6) টাকা = 52 টাকা

মিতার আছে (58+12) টাকা = 70 টাকা।

 

একক কাজ: (পৃষ্টা ২৩৬)

আদর্শ সমীকরণ ax² + bx + c = 0 আকারে লিখ এবং a, b, c এর মান খুঁজে বের করো।

(i) 3x-2x²=7

সমাধানঃ

3x-2x²=7

বা, 3x-2x²-7=0

বা, -2x²+3x-7=0

বা, 2x²-3x+7=0

অতএব, আদর্শ আকার: 2x²-3x+7=0

এবং a,b,c = 2, -3, 7

(ii) (x-7)(x+7)=3x

সমাধানঃ

(x-7)(x+7)=3x

বা, x²-7x+7x-49=3x

বা, x²-49=3x

বা, x²-49-3x=0

বা, x²-3x-49=0

অতএব, আদর্শ আকার: x²-3x-49=0

এবং a,b,c = 1, -3, -49

(iv) 5+2z²=6z

সমাধানঃ

5+2z²=6z

বা, 5+2z²-6z=0

বা, 2z²-6z+5=0

অতএব, আদর্শ আকার: 2z²-6z+5=0

এবং a,b,c = 2, -6, 5

(v) 2x(x-3)=15

সমাধানঃ

2x(x-3)=15

বা, 2x²-6x=15

বা, 2x²-6x-15=0

অতএব, আদর্শ আকার:  2x²-6x-15=0

এবং a,b,c = 2, -6, -15

(vi) 5w(7w-2)=10w+1

সমাধানঃ

5w(7w-2)=10w+1

বা, 35w²-10w=10w+1

বা, 35w²-10w-10w-1=0

বা, 35w²-20w-1=0

অতএব, আদর্শ আকার:  35w²-20w-1=0

এবং a,b,c = 35, -20, -1

(vi) 4y-3y(y)=9

সমাধানঃ

4y-3y(y)=9

বা, 4y-3y²=9

বা, 4y-3y²-9=0

বা, -3y²+4y-9=0

বা, 3y²-4y+9=0

অতএব, আদর্শ আকার:  3y²-4y+9=0

এবং a,b,c = 3, -4, 9

(vii) a+2a²-19=5a²

সমাধানঃ

a+2a²-19=5a²

বা, a+2a²-19-5a²=0

বা, a-3a²-19=0

বা, -3a²+a-19=0

বা, 3a²-a+19=0

অতএব, আদর্শ আকার:  3a²-a+19=0

এবং a,b,c = 3, -1, 19

এই অধ্যায়ের সমাধান লিঙ্কঃ

২২৯ – ২৩১ পৃষ্ঠা (আজানা রাশির সমীকরণ)

২৩১ পৃষ্ঠার একক কাজ (আজানা রাশির সমীকরণ বিধি)

২৩৪ ও ২৩৬ পৃষ্ঠা (দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ) – এই অংশে আলোচিত

২৪১ পৃষ্ঠা (দ্বিঘাত সমীকরণ কাগজ কেটে সমাধান)

 

সপ্তম শ্রেণির অন্যন্য অধ্যায় লিংকঃ

১০ম অধ্যায়

৯ম অধ্যায়

৮ম অধ্যায়

৭ম অধ্যায়

৬ষ্ট অধ্যায়

৫ম অধ্যায়

সপ্তম শ্রেণির সম্পূর্ণ লিঙ্ক