অজানা রাশির সমীকরণ

Admin

16 April

আমরা ৬ষ্ঠ শ্রেণিতে সমীকরণ ও সরল সমীকরণ সম্পর্কে জেনে এসেছি এবং বাস্তবভিত্তিক সমস্যা থেকে সমীকরণ গঠন করতে শিখেছি। সপ্তম শ্রেণির এই অধ্যায়ে আমরা সমীকরণ সমাধানের কিছু বিধি ও প্রয়োগ সম্পর্কে জানব। ৬ষ্ঠ শ্রেণিতে আমরা সরল সমীকরণ সমাধানের জন্য কতগুলো নিয়ম শিখেছিলাম। চলো নিয়ম গুলোর বাস্তব প্রমান করতে চেষ্টা করি। আমরা আমাদের এই অধ্যায়ে অজানা রাশির সমীকরণ কীভাবে পাই তার বাস্তব প্রমান দেখব। তাহলে শুরু করা যাকঃ-

বাস্তব সমস্যায় অজানা রাশির সমীকরণ

# নিচের নির্দেশিত ভারসাম্য থেকে অজানা মানগুলো কী হতে পারে তা চিন্তা করো এবং ফলাফল খাতায় লিখ।

সমাধানঃ

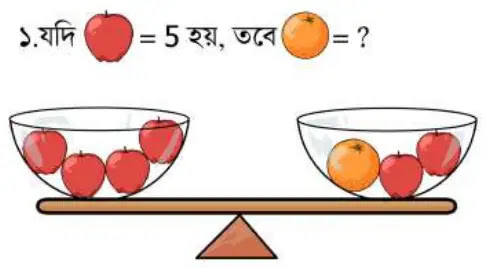
১নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

4টি আপেল = 1টি কমলা লেবু + 2টি আপেল

বা, 4×5 = 1টি কমলা লেবু + 2×5 [শর্তমতে]

বা, 20 = 1টি কমলা লেবু + 10

বা, 1টি কমলা লেবু + 10 = 20

বা, 1টি কমলা লেবু + 10 – 10 = 20 – 10 [উভয়পক্ষ থেকে 10 বিয়োগ করে]

বা, 1টি কমলা লেবু = 10

২নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

3 টি পেয়ারা + 1 টি কলা = 6 পেয়ারা

বা, 3টি পেয়ারা + 1 টি কলা - 3টি পেয়ারা = 6টি পেয়ারা - 3টি পেয়ারা [উভয়পক্ষ থেকে 3টি পেয়ারা বিয়োগ করে]

বা, 1 টি কলা = 3টি পেয়ারা

বা, 1 টি কলা = 3×7

বা, বা, 1 টি কলা = 21

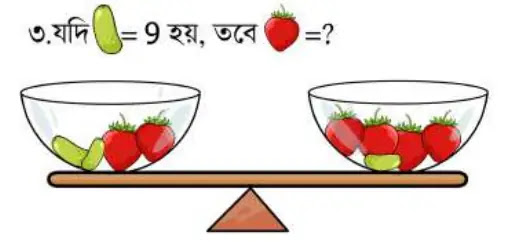
৩নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

2টি শসা + 2টি স্ট্রবেরি = 4টি স্ট্রবেরি + 1টি শসা

বা, 2টি শসা + 2টি স্ট্রবেরি - 1টি শসা = 4টি স্ট্রবেরি + 1টি শসা - 1টি শসা [উভয়পক্ষ থেকে 1টি শসা বিয়োগ করে]

বা, 1টি শসা + 2টি স্ট্রবেরি = 4টি স্ট্রবেরি

বা, 1টি শসা + 2টি স্ট্রবেরি - 2টি স্ট্রবেরি = 4টি স্ট্রবেরি - 2টি স্ট্রবেরি [উভয়পক্ষ থেকে 2টি স্ট্রবেরি বিয়োগ করে]

বা, 1টি শসা = 2টি স্ট্রবেরি

বা, 2টি স্ট্রবেরি = 1টি শসা

বা, 2টি স্ট্রবেরি = 9 [মান বসিয়ে]

বা, 1টি স্ট্রবেরি = ⁹/₂ [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, 1টি স্ট্রবেরি = 4.5

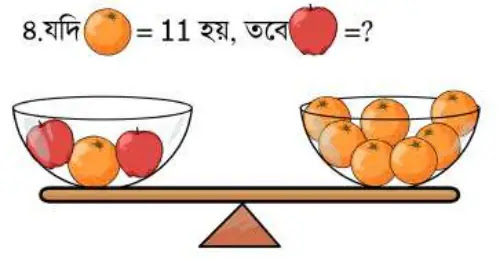
৪নং সমস্যার দাঁড়িপাল্লার ভারসাম্য থেকে লিখতে পারি,

2টি আপেল + 1টি কমলা লেবু = 7টি কমলা লেবু

বা, 2টি আপেল + 1টি কমলা লেবু - 1টি কমলা লেবু = 7টি কমলা লেবু - 1টি কমলা লেবু [[উভয়পক্ষ থেকে 1টি কমলা লেবু বিয়োগ করে]]

বা, 2টি আপেল = 6টি কমলা লেবু

বা, 1টি আপেল = 3টি কমলা লেবু [উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, 1টি আপেল = 3×11

বা, 1টি আপেল = 33

ভারসাম্য সমীকরণ:

একটি সমীকরণের ভারসাম্য বজায় রাখা হবে যদি আমরা :

● উভয় পাশে একই পরিমাণ যোগ করি।

● উভয় পাশ থেকে একই পরিমাণ বিয়োগ করি।

● উভয় পাশকে একই পরিমাণ দিয়ে গুণ করি।

● উভয় পাশকে একই পরিমাণ দিয়ে ভাগ করি।

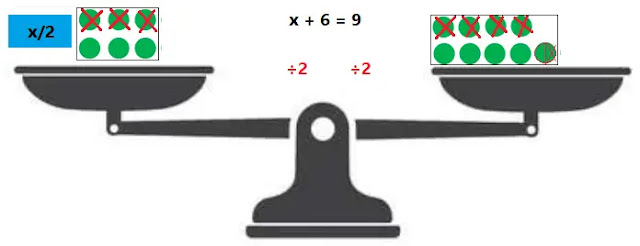
কাজ:

পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির পরিবর্তীত সমীকরণ বের করো এবং গুণ ও ভাগের বিধি নির্ণয় করো।

ক) সমীকরণটির সাথে 3 যোগ করা হয়

খ) সমীকরণটি থেকে 3 বিয়োগ করা হয়

গ) 4 দ্বারা গুণ করা হয়

ঘ) 2 দ্বারা ভাগ করা হয়

সমাধানঃ

ক) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির সাথে 3 যোগ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি। এক্ষেত্রে, প্রিতিটি ধনাত্মক সংখ্যার জন্য পাল্লায় ওজন (●) বৃত্ত সংখ্যা বসাই।

x+6= 9 সমীকরণটির পরিবর্তীত সমীকরণ বের করা

ওজন (●) ব্যবহারের গাণিতিক ধাপসমূহঃ

x + 6 = 9

বা, x + 6 + 3 = 9 + 3

বা, x + 9 = 12

অর্থাৎ, সমীকরণটির সাথে 3 যোগ করা হলে পরিবর্তীত সমীকরণঃ x + 9 = 12

(খ) পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে x+6= 9 সমীকরণটির থেকে 3 বিযোগ করে সাম্যাবস্থায় এনে সমীকরণটির পরিবর্তীত সমীকরণ বের করি। এক্ষেত্রে, প্রিতিটি ধনাত্মক সংখ্যার জন্য পাল্লায় ওজন (●) বৃত্ত সংখ্যা ও ঋণাত্মক সংখ্যার জন্য ওজন (●) বৃত্ত সংখ্যা বসাই।