চলো বৃত্ত চিনি – Class 7 Math BD 2023 – ৮ম অধ্যায় ( ১৬৩ - ১৭০ পৃষ্ঠা)

চলো বৃত্ত চিনি

চলো বৃত্ত চিনি হলো ২০২৩ এর সপ্তম শ্রেণির গণিত পাঠ্যবইয়ের অষ্টম অধ্যায় এর নাম। এই অধ্যায়ে বৃত্ত সম্পর্কে আলোচনা করা হয়েছে। নিচে কিছু বস্তুর ছবি দেয়া হয়েছে। পাঠ্যবইয়ে নিচের আকৃতিগুলো চেনানোর মাধ্যমে চলো বৃত্ত চিনি এর সূচনা করা হয়েছে। আমরা পাঠ্যবইয়ের সমস্যাগুলো সমাধান করবো। তাহলে শুরু করা যাক-

দলগত কাজ: বৃত্তাকার বস্তুর নাম লেখার প্রতিযোগিতা। সময়ঃ ৫ মিনিট। দলের প্রত্যেকে নিজ নিজ খাতায় বৃত্তাকার বস্তুর নাম লিখবে। যে সবচেয়ে বেশি নাম লিখতে পারবে, সে জয়লাভ করবে।

সমাধানঃ

কে জয়লাভ করবে তাহা শিক্ষক বিচার করবেন। আমরা এখানে শুধু কিছু বৃত্তাকার বস্তুর নাম তুলে ধরলাম।

1. চাকা
2. ডিস্ক
3. বোতাম
4. মেডেল বা পদক
5. দেয়াল ঘড়ি
6. সিডি
7. লেন্স
8. পিজ্জা
9. প্যানকেক
10. চাঁদ
11. সূর্য
12. বৃত্তাকার পথ
13. প্লেট
14. বাটি
15. আপেল
16. বল
17. সাইকেল চাকা
18. চুড়ি
19. কয়েন
20. কন্টাক্ট লেন্স
21. জারের ঢাকনা
22. প্লেট
23. সূর্যমুখী
24. কয়ল
25. গ্লোব ইত্যাদি।

দলগত কাজ:

কতগুলো ছোট ছোট দলে বিভক্ত হয়ে বিভিন্ন দৈর্ঘ্যের দড়ি ব্যবহার করে মাটিতে দিশার মতো বৃত্ত তৈরি করো। দলগুলোর নাম দাও। প্রত্যেক দলের তৈরি করা বৃত্তগুলো পর্যবেক্ষণ করো এবং নিচের প্রশ্নগুলোর উত্তর খাতায় লিখ।

1. কোন দল সবচেয়ে ছোট বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য কত মিটার?
2. কোন দল সবচেয়ে বড় বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য কত মিটার?
3. দড়ির দৈর্ঘ্য বেশি হলে বৃত্তটির আকার কীরূপ হবে, যুক্তিসহ ব্যাখ্যা করো।

সমাধানঃ

আমাদের ছোট ছোট দলে বিভক্ত দলগুলোর নাম ও ব্যবহৃত দড়ির দৈর্ঘ্য হলোঃ

দলের নাম	দড়ির দৈর্ঘ্য (মিটার)
অর্জুন দল	১ মিটার
শাপলা দল	১.৫ মিটার
জবা দল	২ মিটার
আপেল দল	২.৫ মিটার

প্রশ্নগুলোর উত্তরঃ

1. অর্জুন দল সবচেয়ে ছোট বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য ১ মিটার।
2. আপেল দল সবচেয়ে বড় বৃত্ত তৈরি করেছে এবং তাদের ব্যবহার করা দড়ির দৈর্ঘ্য ২.৫ মিটার।
3. দড়ির দৈর্ঘ্য যত বেশি হবে বৃত্তের আকার তত বড় হবে। ব্যাখ্যাঃ এখানে দড়ির দৈর্ঘ্য বৃত্তের ব্যাসার্ধ হিসেবে কাজ করে আর আমরা জানি বৃত্তের ব্যাসার্ধ যত বেশি হবে বৃত্তটিও তত বড় হবে।

একক কাজ: প্রত্যেকেই মীরার মতো চূড়ি ব্যবহার করে বৃত্তাকার কাগজ কেটে কেন্দ্র নির্ণয় করো। চূড়ির পরিবর্তে কাপ বা গ্লাস বা অন্যকোনো বস্তু দ্বারাও বৃত্তাকার কাগজ কেটে নিতে পারবে। তাছাড়া কেন্দ্র নির্ণয়ে অন্য কোনো পদ্ধতিও ব্যবহার করতে পারবে।

সমাধানঃ

আমি আমার খাতায় একটি চুড়ি বসিয়ে চুড়ির মাপে কাগজ কেটে নেই। ফলে একটি কাগজের বৃত্ত পেয়ে গেলাম।

কাগজের বৃত্তের কেন্দ্র নির্ণয়ঃ

কাগজটিকে প্রথমে চিত্রের মত করে দুইটি ভাঁজ দিয়ে সমান চার ভাগে ভাঁজ করি। দুইটি ভাঁজের ছেদবিন্দু চিহ্নিত করি। তাহলে উক্ত ছেদবিন্দুটিই হলো কাগজের বৃত্তের কেন্দ্র।

দলগত কাজ:

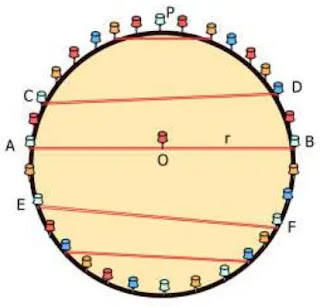
চিত্রের মতো কাগজে একটি বৃত্ত আঁক। তারপর বৃত্তের উপর কতগুলো পিন বসিয়ে নাও। লক্ষ রাখবে, ব্যাসের দুই প্রান্তে বৃত্তের উপর যেন দুইটি পিন থাকে। রাবার দিয়ে চিত্রের মতো ব্যাস ও জ্যা তৈরি করো। প্রয়োজনে পিনগুলোর গোড়ায় বিন্দু দিয়ে চিহ্নিত করো। তারপর বৃত্তের ব্যাসার্ধ, জ্যা, উপচাপ, অধিচাপ, অর্ধবৃত্তসহ সকল অঙ্গ নিয়ে সকলে আলোচনা করো। স্কেল ও সূতা ব্যবহার করে বৃত্তের ব্যাসার্ধ, ব্যাস, জ্যা, বৃত্তচাপ মেপে খাতায় লিখ। এবার নিচের প্রশ্নগুলোর উত্তর খজেুঁ দেখোঃ

(১) বৃত্তের ব্যাস ও ব্যাসার্ধের মর্ধ্যে সম্পর্ক কী? 

(২) বৃত্তের কোন জ্যা-টি সবচেয়ে বড়?

(৩) সবচেয়ে বড় জ্যাটিকে আমরা কী বলে থাকি?

(৪) বৃত্তের ব্যাস বৃত্তকে দুই ভাগে ভাগ করেছে তাদের দৈর্ঘ্য কীরূপ? 

(৫) বৃত্তের ব্যাস দ্বারা সৃষ্ট চাপ দুইটির প্রত্যেকটিকে কী বলা হয়?

সমাধানঃ

চিত্রের মতো কাগজে একটি বৃত্ত আঁকলাম। তারপর বৃত্তের উপর কতগুলো পিন বসিয়ে নিলাম। ব্যাস বরাবর দুই প্রান্তে দুইটি পিন রাখলাম। রাবার দিয়ে চিত্রের মতো ব্যাস ও জ্যা তৈরি করলাম। এবং পিনগুলোর গোড়ায় বিন্দু লিখে চিহ্নিত করলাম।

স্কেল ও সূতা ব্যবহার করে বৃত্তের ব্যাসার্ধ, ব্যাস, জ্যা, বৃত্তচাপ মেপে খাতায় লিখলাম। মাপগুলো নিন্মরুপঃ

ব্যাসার্ধ	২ সেমি
ব্যাস	৪ সেমি
জ্যা	৩ সেমি, ৩.২ সেমি, ২ সেমি, ১.৪ সেমি, ০.৫ সেমি।
বৃত্তচাপ	৩ সেমি, ৩.২ সেমি, ২.২ সেমি ইত্যাদি

(১) বৃত্তের ব্যাস ও ব্যাসার্ধের মধ্য সম্পর্কঃ বৃত্তের ব্যাস তার ব্যাসার্ধের দ্বিগুণ।

(২) বৃত্তের যে জ্যা-টি বৃত্তের কেন্দ্র দিয়ে যায় সেটি সবচেয়ে বড় জ্যা। উল্লেখ্য ব্যাসও একটি জ্যা অর্থাৎ ব্যাসই বৃত্তের সবচেয়ে বড় জ্যা।

(৩) সবচেয়ে বড় জ্যাটিকে আমরা ব্যাস বলে থাকি।

(৪)বৃত্তের ব্যাস বৃত্তকে দুই ভাগে ভাগ করেছে তাদের দৈর্ঘ্য সমান।

(৫)বৃত্তের ব্যাস দ্বারা সৃষ্ট চাপ দুইটির প্রত্যেকটিকে অর্ধচাপ বলে।

একক কাজ:

১. কাগজ কেটে নিচের চিত্রের মতো বৃত্তের কেন্দ্র, ব্যাসার্ধ, জ্যা এবং পরিধি তৈরি করো।

সমাধানঃ

চিত্র অনুসারে নিজে চেষ্টা করো।

২. পেন্সিল কম্পাসের সাহায্যে খাতায় বিভিন্ন মাপের কয়েকটি বৃত্ত আঁক। বৃত্তগুলোর কেন্দ্র চিহ্নিত করো। বৃত্তগুলোর উপরে বিভিন্ন জায়গায় কয়েকটি বিন্দু নিয়ে কেন্দ্র থেকে বিন্দুগুলো পর্যন্ত রেখাংশগুলো আঁক। প্রতিটি বৃত্তের কেন্দ্রগামী জ্যা বা ব্যাস আঁক। এবার খাতায় নিচের ছক বা সারণিটি তৈরি করো। প্রতিটি বৃত্তের ব্যাসার্ধ কেন্দ্রগামী জ্যা বা ব্যাসের দৈর্ঘ্য পরিমাপ করে সারণিটি পূরণ করো এবং সহপাঠির সাথে ফলাফল নিয়ে আলোচনা করো।

সমাধানঃ

পেন্সিল কম্পাসের সাহায্যে চারটি বৃত্ত আঁকলাম। বৃত্তচারটির কেন্দ্র যথাক্রমে A, B, C, D চিহ্নিত করলাম। বৃত্তের উপরে বিভিন্ন বিন্দু নিয়ে কেন্দ্র থেকে বিন্দুগুলো পর্যন্ত রেখাংশগুলো আঁকলাম এবং তার সাথে প্রত্যেকটি বৃত্তে ব্যাস আঁকলাম। অতপর বৃত্তগুলোর ব্যাসার্ধ ও ব্যাসের দৈর্ঘ্য পরিমাপ করে প্রদত্ত সারণিটি পুরন করে সহপাঠির সাথে ফলাফল নিয়ে আলোচনা করলাম।

পুরণকৃত সারণি ও ফলাফল নিন্মরুপঃ

বৃত্ত	কেন্দ্র থেকে বৃত্তের দৈর্ঘ্য বা ব্যাসার্ধ	কেন্দ্রগামী জ্যায়ের দৈর্ঘ্য বা ব্যাসের দৈর্ঘ্য	ফলাফল পর্যবেক্ষন করে বৃত্তের ব্যাসার্ধ ও কেন্দ্রগামী জ্যা বা ব্যাস এর মধ্যকার সম্পর্ক বর্ণনা
১.	১ সেমি	২ সেমি	ব্যাস = ২xব্যাসার্ধ
২.	১.৫ সেমি	৩ সেমি	ব্যাস = ২xব্যাসার্ধ
৩.	২ সেমি	৪ সেমি	ব্যাস = ২xব্যাসার্ধ
৪.	২.৫ সেমি	৫ সেমি	ব্যাস = ২xব্যাসার্ধ

৩. কাগজ কেটে ৩ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট পাঁচটি বৃত্ত তৈরি করো। বৃত্তগুলোকে নিচের চিত্রের মতো সাজিয়ে কেন্দ্রগুলো যোগ করে ইংরেজি বর্ণ W আকৃতিটি বানাও। এবার A থেকে B পর্যন্ত দৈর্ঘ্য নির্ণয় করো। C কেন্দ্রবিশিষ্ট বৃত্তটির চার পাশে এভাবে সর্বোচ্চ কয়টি বৃত্ত সাজানো যাবে?

সমাধানঃ

কাগজ কেটে ৩ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট পাঁচটি বৃত্ত তৈরি করলাম। বৃত্তগুলোকে নিচের চিত্রের মতো সাজিয়ে কেন্দ্রগুলো যোগ করে ইংরেজি বর্ণ W আকৃতিটি বানালাম।

A থেকে B পর্যন্ত দৈর্ঘ্য নির্ণয়ঃ

চিত্রে, A, C ও B কেন্দ্রবিশিষ্ট তিনটি বৃত্ত পাশাপাশি অবস্থান করছে যেখানে প্রত্যেকটি বৃত্তের ব্যসার্ধ হলো ৩ সেমি।

তাহলে,

A থেকে C এর দূরত্ব

= A কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ + C কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ

= ৩ সেমি + ৩ সেমি

= ৬ সেমি।

আবার,

C থেকে B এর দূরত্ব

= C কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ + B কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধ

= ৩ সেমি + ৩ সেমি

= ৬ সেমি।

অতএব, A থেকে B এর দূরত্ব = ৬ সেমি + ৬ সেমি = ১২ সেমি।

C কেন্দ্রবিশিষ্ট বৃত্তটির চার পাশে এভাবে সর্বোচ্চ যতগুলি বৃত্ত সাজানো যাবে তাহা নির্ণয়:

চিত্র অনুসারে, C এর বাম পাশে একটি বৃত্ত আছে এবং সেই অনুসারে ডানপাশেও একটি বৃত্ত আছে।

অর্থাৎ, বাম ও ডান পাশে মোট বৃত্তের সংখ্যা ২টি।

আবার,

C এর নিচে ২টি বৃত্ত আছে, সেই অনুসারে C এর উপরেও ২টি বৃত্ত একইভাবে সাজানো যাবে।

তাহলে, C এর উপরে ও নিচে মোট বৃত্ত সাজানো যাবে ২+২ টি = ৪টি।

অতএব,

C এর চারপাশে অর্থাৎডানে-বামে এবং উপরে নিচে মোট বৃত্ত সাজানো যাবে

= ২টি + ৪টি

= ৬টি।

এই অধ্যায়ের অংশসমূহঃ

১৬৩ - ১৭০ পৃষ্ঠা (চলো বৃত্ত চিনি) - এই অংশে লিখিত

১৭১ - ১৭৬ পৃষ্ঠা (বৃত্তের পরিধি)

১৭৬ - ১৮২ পৃষ্ঠা (বৃত্তের ক্ষেত্রফল)

৭ম শ্রেণির গণিতের অন্যান্য অধ্যায়ের লিঙ্কঃ

৩য় অধ্যায়

৪র্থ অধ্যায়

৫ম অধ্যায়

৭ম শ্রেণির গনিতের সকল অধ্যায়