Amar Ganit Class 4 – দল গড়ে খেলি – সমতুল্য পাঠ ২৪ – পাতা (১৮৭-২০১)
দল গড়ে খেলি
বন্ধুরা আমরা এই পাঠ দল গড়ে খেলি অংশকে সমতুল্য পাঠ আকারে
তুলে ধরেছি। আমরা মূলত মূল বিষয়বস্তু এখানে তুলে ধরেছি এবং সকল প্রশ্নের উত্তর প্রদান
করেছি। চল শুরু করিঃ- পীযুষ ও পলাশ একই গ্রামে বাস করে। তাদের গ্রামের নাম কাঁটামণি।
তারা প্রতিদিন বিকাল বেলায় মাঠে খেলা করে। তারা ও তার বন্ধুরা মিলে দল গড়ে খেলা করে।
আজ পীযুষ ও পলাশ মাঠে এসেছে।
এখন মাঠে মাত্র তারা ২ জন।
২-এর উৎপাদকঃ ১ ও ২
তাই তারা ১ জন বা ২ জনের দল গঠন করতে পারবে।
একটু পর প্রিতম তাদের সঙ্গে যোগ দিল। তারা মোট ৩ জন হলো।
৩-এর উৎপাদকঃ ১, ৩
তাই তারা ১ জন বা ৩ জনের দল গঠন করতে পারবে।
একটু পর আরও ১ জন আসলে তারা সংখ্যায় মোট ৪ জন হলো।
৪-এর উৎপাদকঃ ১, ২ ও ৪
তাই, তারা ১, ২ বা ৪ জনের দল গঠন করতে পারবে।
অনুরুপভাবে,
৫-এর উৎপাদকঃ ১ ও ৫
তাই, ১ বা ৫ জনের দল গঠন করতে পারবে।
ফলাফলঃ তারা কিছু ক্ষেত্রে ২ রকমভাবে দল গড়তে পারবে আবার
কিছু ক্ষেত্রে ২ এর অধিক রকমভাবে দল গঠন করতে পারবে। এরকম কেন হয়?
কারণঃ
যেসকল সংখ্যার বেলায় দুইটি মাত্র দল গঠন করা যায় তারা মৌলিক সংখ্যা আর যাদের ক্ষেত্রে দুইয়ের অধিক দল গঠন করা যায় তারা যৌগিক সংখ্যা। চল, মৌলিক ও যৌগিক সংখ্যা নিয়ে আরো একটু জানি।
মৌলিক সংখ্যাঃ কিছু সংখ্যা আছে যাদের গুণনীয়ক বা
উৎপাদক ১ এবং সেই সংখ্যা তাদেরকে মৌলিক সংখ্যা বলে।
যৌগিক সংখ্যাঃ যাদের ২টির বেশি উৎপাদক বা গুণনীয়ক
থাকবে তাদেরকে যৌগিক সংখ্যা বলে।
১ কি মৌলিক না যৌগিক সংখ্যাঃ
১-এর উৎপাদক ১; ১-এর গুণনীয়কের সংখ্যা ১টি।
যেহেতু ১-এর গুণনীয়কের সংখ্যা ২টিও নয় বা ২-এর অধিকও নয়,
তাই ১ মৌলিক সংখ্যাও নয় আবার যৌগিক সংখ্যাও নয়।
উপরের আলোচনা থেকে বুঝলামঃ
২,৩,৫ হলো মৌলিক সংখ্যা কারণ এদের প্রত্যেকের গুণনীয়কের
সংখ্যা ২টি করে আছে।
আবার,
৪ হলো যৌগিক সংখ্যা কারণ এর ২টির বেশী গুণনীয়ক আছে।
নিচের সংখ্যা তিনটি মৌলিক না যৌগিক বিচার করি।
৬,৭,৮
বিচারঃ
৬ এর গুণনীয়কঃ ১,২,৩,৬
৬-এর গুণনীয়কের সংখ্যা ৪টি।
∵ ৬-একটি যৌগিক সংখ্যা।
৭-এর গুণনীয়কঃ ১,৭
অর্থাৎ এর গুণনীয়কের সংখ্যা ২টি।
∵ ৭-একটি মৌলিক সংখ্যা ।
৮-এর গুণনীয়কঃ ১,২,৪,৮
অর্থাৎ এর গুণনীয়কের সংখ্যা ৪টি।
∵ ৮-একটি যৌগিক সংখ্যা ।
নিজে করি [পাতা-১৮৯]
নিচের সংখ্যাগুলোর কোনগুলো মৌলিক সংখ্যা আর কোনগুলো যৌগিক
সংখ্যা তা নির্ণয় করিঃ
৯,১০,১১,১২ ও ১৪
সমাধানঃ
|
প্রদত্ত সংখ্যা
|
উৎপাদকগুলি
|
উৎপাদকের সংখ্যা
|
|
৯
|
১,৩,৯
|
৩টি
|
|
১০
|
১,২,৫,১০
|
৪টি
|
|
১১
|
১,১১
|
২টি
|
|
১২
|
১,২,৩, ৪,৬,১২
|
৬টি
|
|
১৪
|
১,৭,১৪
|
৩টি
|
সিদ্ধান্তঃ উৎপাদকের সংখ্যা হতে পাই, ১১-এর উৎপাদকের সংখ্যা
২টি এবং বাকীগুলোর ২টির অধিক। তাহলে, ১১ হলো মৌলিক সংখ্যা এবং ৯,১০,১২,১৪ হলো যৌগিক
সংখ্যা।
হাতেকলমে [পাতা-১৮৯]
হাতেকলমে ১ থেকে ১০ পর্যন্ত সংখ্যার গুণিতক, গুণনীয়ক খুঁজি
ও কোনগুলি মৌলিকসংখ্যা দেখি।
সমাধানঃ
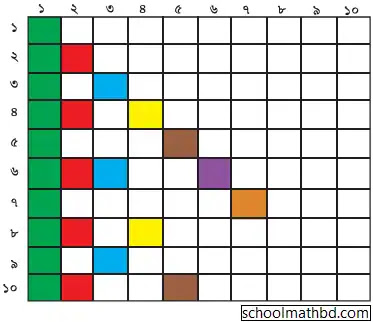
আমি একটি ১০০টি সমান ঘর কাটা বর্গক্ষেত্রাকার কাগজ নিলাম।
যার উপরে ও পাশে ১ থেকে ১০ পর্যন্ত লেখা আছে।
ছবির মতো,
লম্বালম্বিভাবে- ১-এর প্রতি ঘরে সবুজ রং দিলাম, ২-এর শুরু
থেকে ১ ঘর অন্তর লাল রং দিলাম, ৩-এর শুরু থেকে ২ ঘর অন্তর নীল রং দিলাম। এভাবে ৪,৫,৬,৭,৮,৯,১০
এর জন্য ৩,৪,৫,৬,৭,৮,৯ ঘর অন্তর হলুদ, বাদামি, বেগুনি, কমলা সহ নানান রং দিলাম।
পেলাম,
লম্বালম্বিভাবে, সব সবুজ রঙের ঘরগুলো হলো ১-এর গুণিতকগুলো।
অর্থাৎ ১,২,৩,৪,……..
এভাবে বিভিন্ন রঙের ঘরগুলো হতে ২,৩,৪,৫,৬,৭,৮,৯,১০-এর গুণিতকগুলো
পেলাম। যেমনঃ ২-এর গুণিতকগুলোঃ ২,৪,৬,৮,১০। ৩-এর গুণিতকগুলোঃ ৩,৬,৯।
আবার,
পাশাপাশিভাবে, ১-এর সারিতে রঙ্গিন ঘর পেলাম ১টি যার নাম্বার
১। অর্থাৎ ১ এর উৎপাদকঃ ১।
২-এর সারিতে রঙিন
ঘর পেলাম ২টি যার নাম্বার ১,২। অর্থাৎ ২ এর উৎপাদকগুলোঃ ১,২।
৩-এর সারিতে রঙিন ঘর পেলাম ২টি যার নাম্বার ১,৩। অর্থাৎ
৩-এর উৎপাদকগুলোঃ ১,৩।
অনুরুপভাবে পেলামঃ
|
সংখ্যা
|
উৎপাদকগুলো
|
উৎপাদকের সংখ্যা
|
|
৪
|
১,২,৪
|
৩টি
|
|
৫
|
১,৫
|
২টি
|
|
৬
|
১,২,৩,৬
|
৪টি
|
|
৭
|
১,৭
|
২টি
|
|
৮
|
১,২,৪,৮
|
৪টি
|
|
৯
|
১,৩,৯
|
৩টি
|
|
১০
|
১,২,৫,১০
|
৪টি
|
মৌলিক সংখ্যা নির্ণয়ঃ দেখলাম ২,৩,৫ ও ৭ এর উৎপাদকের সংখ্যা
আছে ২টি করে অর্থাৎ ২,৩,৫,৭ হলো মৌলিক সংখ্যা।
অপরদিকে, ৪,৬,৮,৯,১০-এর উৎপাদকের সংখ্যা আছে ২টির অধিক
অর্থাৎ এরা যৌগিক সংখ্যা।
কিন্তু, ১-এর উৎপাদকের সংখ্যা ১টি, তাই ১ হলো না মৌলিক
না যৌগিক।
নিজে করি
[পাতা-১৯০]
একইভাবে নানা রং বা চিহ্ন দিয়ে ১ থেকে ২০ পর্যন্ত সংখ্যার
মধ্যে মৌলিক সংখ্যা খুঁজি।
সমাধানঃ
আমি একটি ৪০০টি সমান ঘর কাটা বর্গক্ষেত্রাকার কাগজ নিলাম।
যার উপরে ও পাশে ১ থেকে ২০ পর্যন্ত লেখা আছে।
ছবির মতো,
লম্বালম্বিভাবে- ১-এর প্রতি ঘরে, ২-এর শুরু থেকে ১ ঘর অন্তর,
৩-এর শুরু থেকে ২ ঘর অন্তর বিভিন্ন রং দিলাম। এভাবে ৪,৫,….১৯,২০ এর জন্য ৩,৪,…….,১৮,১৯
ঘর নানান রং দিলাম।
এখন, পাশাপাশিভাবে ঘরগুলি লক্ষ্য করি এবং দেখি প্রতিটি
সংখ্যা (১ থেকে ২০) এর ডানের ঘরগুলির মধ্যে শুধুমাত্র দুটি ঘর রঙিন হয়েছে কোনগুলি।
পেলাম, এরুপ রঙিন হয়েছে ২,৩,৫,৭,১১,১৩,১৭ ও ১৯-এর ঘরগুলি।
অর্থাৎ, ১ থেকে ২০ পর্যন্ত সংখ্যার মধ্যে মৌলিক সংখ্যা
২,৩,৫,৭,১১,১৩,১৭ ও ১৯।
= ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯।
আমি ১ থেকে ১০০ পর্যন্ত সংখ্যার মধ্যে মৌলিক সংখ্যা খুঁজি
[পাতা-১৯১]।
(১) প্রথমে ১-কে ‘/’এই দাগ দিয়ে কাটি, কারণ ১ মৌলিক সংখ্যাও
নয় এবং যৌগিক সংখ্যাও নয়।
(২) এরপর ২-কে ‘○’-এভাবে গোল করি এবং ২ ছাড়া ২-এর অন্য গুণিতকগুলি
অর্থাৎ ৪,৬,৮,….এগুলিকে ‘/’এই দাগ কাটি।
(৩) দেখলাম ২-এর ঠিক পরবর্তী সংখ্যা হলো ৩-যেটাকে কাটা
হয়নি। ৩-কে ‘○’-এভাবে
গোল করি এবং ৩ ছাড়া ৩-এর অন্য গুণিতকগুলি অর্থাৎ ৬,৯,১২,…..এগুলিকে ‘/’এই দাগ দিয়ে
কাটি।
(৪) দেখলাম ৩-এর ঠিক পরবর্তী সংখ্যা হলো ৫-যেটাকে কাটা
হয়নি। ৫-কে ‘○’-এভাবে
গোল করি এবং ৫ ছাড়া ৫-এর অন্য গুণিতকগুলি অর্থাৎ ১০,১৫,২০,…..এগুলিকে ‘/’এই দাগ দিয়ে
কাটি।
(৫) এভাবে যতক্ষন না পর্যন্ত ওই ছকের সমস্থ সংখ্যা ‘/’এই
দাগ দিয়ে কাটছি অথবা ‘○’-এভাবে
গোল করছি, ততক্ষন পর্যন্ত উপরের পদ্ধতি করে যাই।
ওই ছকের সমস্থ ‘○’-এভাবে গোল করা সংখ্যাগুলি হলো মৌলিক সংখ্যা
এবং ‘/’এই দাগ দিয়ে কাটা (১ ছাড়া) সংখ্যাগুলি হলো যৌগিক সংখ্যা।
গ্রিক গণিতজ্ঞ ইরাটোস্থিনিস (Eratosthenes) খ্রিস্টপূর্ব
তৃতীয় শতকে কোনো সংখ্যার গুণনীয়ক বা উৎপাদক বার না করে সহজেই ১ থেকে ১০০ পর্যন্ত সংখ্যার
মধ্যে মৌলিক সংখ্যা খোঁজার এই পদ্ধতি বলেছিলেন।
এই পদ্ধতিকে ইরাটোস্থিনিসের চালুনি (Sieve of
Eratosthenes) বলা হয়।
ইরাটোস্থিনিসের চালুনি পদ্ধতিতে ১ থেকে ১০০-এর মধ্যে কোনগুলি মৌলিক সংখ্যা পেলাম তা লিখি।
উত্তরঃ
_২_, _৩_, _৫_, _৭_, _১১_, _১৩_, _১৭_, _১৯_, _২৩_, _২৯_, _৩১_, _৩৭_, _৪১_, _৪৩_, _৪৭_, _৫৩_, _৫৯_, _৬১_, _৬৭_, _৭১_, _৭৩_, _৭৯_, _৮৩_, _৮৯_ ও _৯৭_।
ফলাফলঃ
২ ছাড়া অন্য সকল মৌলিক সংখ্যাই হলো বিজোড়। অর্থাৎ একমাত্র জোড় মৌলিক সংখ্যা হলো ২ এবং তা মৌলিক সংখ্যাগুলির
মধ্যে সবচেয়ে ছোটো।
আবার অনেক পরপর বিজোড় সংখ্যা মৌলিক সংখ্যা যেমন ৩,৫ - ১১,১৩ - ১৭,১৯ - ২৯,৩১ - ৪১,৪৩ - ৫৯,৬১ - ৭১,৭৩ যাদেরকে যমজ মৌলিক সংখ্যা বলা হয়।
৭ একটি মৌলিক সংখ্যা। ৭-এর পরের মৌলিক সংখ্যা হলো ১১। তবে কি ৭ ও ১১-কে যমজ মৌলিক সংখ্যা বলব?
সমাধানঃ
না, ৭ ও ১১ যমজ মৌলিক সংখ্যা নয়। কারণ ৭-এর পরের বিজোড়
সংখ্যা ৯; কিন্তু ৯ মৌলিক সংখ্যা নয়। যদি ৭-এর পরের বিজোড় সংখ্যা মৌলিক হতো তখন ৭ ও
সেই সংখ্যা যমজ মৌলিক সংখ্যা হতো।
ফলাফলঃ যমজ মৌলিক সংখ্যা হলো সেই দুটি মৌলিক সংখ্যা যাদের
বিয়োগফল ২।
গাছের ফলে মৌলিক সংখ্যা লিখি [পাতা-১৯৩]
|
সংখ্যা
|
গুণনীয়কগুলি
|
|
২
|
১,২
|
|
১৭
|
১,১৭
|
|
২৩
|
১,২৩
|
|
৭
|
১,৭
|
পেলাম, সকল মৌলিক সংখ্যার একটি সাধারণ গুণনীয়ক আছে যা হলো
১।
অন্য দুটি আলাদা মৌলিক সংখ্যা নিয়ে তাদের সাধারণ গুণনীয়ক
খুঁজি।
সমাধানঃ
২-এর গুণনীয়কগুলোঃ ১,২
৭-এর গুণনীয়কগুলোঃ ১,৭
এদের সাধারণ গুণনীয়কঃ ১
পাথরের গায়ে যৌগিক সংখ্যা লিখি [পাতা-১৯৪]
|
সংখ্যা
|
গুণনীয়কগুলো
বা উৎপাদকগুলো
|
|
৬
|
১,২,৩,৬
|
|
২১
|
১,৩,৭,২১
|
|
৮
|
১,২,৪,৮
|
|
৯
|
১,৩,৯
|
ফলাফলঃ
৬ ও ২১ এর সাধারণ উৎপাদকগুলোঃ ১,৩
৮ ও ৯ এর সাধারণ উৎপাদকগুলোঃ ১
ফলত, দুটি যৌগিক সংখ্যারও সাধারণ উৎপাদক বা গুণনীয়ক ১ হতে
পারে। তাহলে বল তো দুটি সংখ্যার সাধারণ গুণনীয়ক ১ হলে তাদের কি সংখ্যা বলব?
উত্তরঃ
দুটি সংখ্যার সাধারণ গুণনীয়ক ১ হলে তাদের পরস্পর মৌলিক
সংখ্যা বলা হয়।
নিজে করি [পাতা-১৯৫]
১. মৌলিক সংখ্যা হলে ফুলে সবুজ রং ও যৌগিক সংখ্যা হলে ফুলে
লাল রং দিই।
|
২১❀
|
৩১❀
|
৪২❀
|
১৩❀
|
|
৩৬❀
|
৪৯❀
|
৯১❀
|
২২❀
|
সমাধানঃ
|
২১❀
|
৩১❀
|
৪২❀
|
১৩❀
|
|
৩৬❀
|
৪৯❀
|
৯১❀
|
২২❀
|
২. ১ থেকে ২০০ পর্যন্ত ছক করে ‘ইরাটোস্থিনিসের চালুনি’
পদ্ধতিতে মৌলিক সংখ্যা খুঁজে বার করি।
সমাধানঃ
|
১
|
৪১
|
৮১
|
১২১
|
১৬১
|
|
২
|
৪২
|
৮২
|
১২২
|
১৬২
|
|
৩
|
৪৩
|
৮৩
|
১২৩
|
১৬৩
|
|
৪
|
৪৪
|
৮৪
|
১২৪
|
১৬৪
|
|
৫
|
৪৫
|
৮৫
|
১২৫
|
১৬৫
|
|
৬
|
৪৬
|
৮৬
|
১২৬
|
১৬৬
|
|
৭
|
৪৭
|
৮৭
|
১২৭
|
১৬৭
|
|
৮
|
৪৮
|
৮৮
|
১২৮
|
১৬৮
|
|
৯
|
৪৯
|
৮৯
|
১২৯
|
১৬৯
|
|
১০
|
৫০
|
৯০
|
১৩০
|
১৭০
|
|
১১
|
৫১
|
৯১
|
১৩১
|
১৭১
|
|
১২
|
৫২
|
৯২
|
১৩২
|
১৭২
|
|
১৩
|
৫৩
|
৯৩
|
১৩৩
|
১৭৩
|
|
১৪
|
৫৪
|
৯৪
|
১৩৪
|
১৭৪
|
|
১৫
|
৫৫
|
৯৫
|
১৩৫
|
১৭৫
|
|
১৬
|
৫৬
|
৯৬
|
১৩৬
|
১৭৬
|
|
১৭
|
৫৭
|
৯৭
|
১৩৭
|
১৭৭
|
|
১৮
|
৫৮
|
৯৮
|
১৩৮
|
১৭৮
|
|
১৯
|
৫৯
|
৯৯
|
১৩৯
|
১৭৯
|
|
২০
|
৬০
|
১০০
|
১৪০
|
১৮০
|
|
২১
|
৬১
|
১০১
|
১৪১
|
১৮১
|
|
২২
|
৬২
|
১০২
|
১৪২
|
১৮২
|
|
২৩
|
৬৩
|
১০৩
|
১৪৩
|
১৮৩
|
|
২৪
|
৬৪
|
১০৪
|
১৪৪
|
১৮৪
|
|
২৫
|
৬৫
|
১০৫
|
১৪৫
|
১৮৫
|
|
২৬
|
৬৬
|
১০৬
|
১৪৬
|
১৮৬
|
|
২৭
|
৬৭
|
১০৭
|
১৪৭
|
১৮৭
|
|
২৮
|
৬৮
|
১০৮
|
১৪৮
|
১৮৮
|
|
২৯
|
৬৯
|
১০৯
|
১৪৯
|
১৮৯
|
|
৩০
|
৭০
|
১১০
|
১৫০
|
১৯০
|
|
৩১
|
৭১
|
১১১
|
১৫১
|
১৯১
|
|
৩২
|
৭২
|
১১২
|
১৫২
|
১৯২
|
|
৩৩
|
৭৩
|
১১৩
|
১৫৩
|
১৯৩
|
|
৩৪
|
৭৪
|
১১৪
|
১৫৪
|
১৯৪
|
|
৩৫
|
৭৫
|
১১৫
|
১৫৫
|
১৯৫
|
|
৩৬
|
৭৬
|
১১৬
|
১৫৬
|
১৯৬
|
|
৩৭
|
৭৭
|
১১৭
|
১৫৭
|
১৯৭
|
|
৩৮
|
৭৮
|
১১৮
|
১৫৮
|
১৯৮
|
|
৩৯
|
৭৯
|
১১৯
|
১৫৯
|
১৯৯
|
|
৪০
|
৮০
|
১২০
|
১৬০
|
২০০
|
প্রক্রিয়াঃ
(১) ছকে ১ থেকে ২০০ পর্যন্ত সংখ্যা লিখি।
(২) আমরা জানি ১ মৌলিক ও যৌগিক কোনটাই নয়। তাই ১-কে রঙে
রঙিন করি।
(৩) ১-এর পরবর্তী সংখ্যা ২-এর গুণিতকগুলোকে (৪,৬,৮,….২০০)
রঙিন করি।
(৪) এরপর দেখি ২-এর পরে ৩ রঙিন হয় নাই, এবার ৩-এর গুণিতকগুলোকে
(৯,১৫,২১,…..১৯৮) রঙিন করি।
(৫) এবার দেখি ৩-এর পরে ৭ রঙিন হয় নাই, ৭-এর গুণিতকগুলোকে
(১৪,২১,….) রঙিন করি।
(৬) এবার দেখি ৭-এর পরে ১১ রঙিন হয় নাই, ১১-এর গুণিতকগুলো
(২২,৩৩,……) রঙিন করি।
(৮) এবার দেখি ১১-এর পরে ১৩ রঙিন হয় নাই, ১৩-এর গুণিতকগুলো
(২৩,৩৯,…..) রঙিন করি।
(৯) এরপর দেখি ১৩-এর পর ১৭ রঙিন হয় নাই কিন্তু ১৭২=২৮৯>২০০;
তাই ধাপ ৮ পর্যন্ত রঙিন করা যথেষ্ট।
(১০) এবার যে সংখ্যাগুলো রঙিন করা হয় নাই সেগুলো হলো ১
থেকে ২০০ পর্যন্ত প্রাপ্ত মৌলিক সংখ্যা।
অতএব, ১ থেকে ২০০ পর্যন্ত মৌলিক সংখ্যাগুলো হলোঃ
২,৩, ৫,৭, ১১,১৩, ১৭,১৯, ২৩,২৯, ৩১,৩৭, ৪১,৪৩, ৪৭,৫৩, ৫৯,৬১, ৬৭,৭১, ৭৩,৭৯, ৮৩,৮৯, ৯৭,১০১, ১০৩,১০৭, ১০৯,১১৩, ১২৭,১৩১, ১৩৭,১৩৯, ১৪৯,১৫১, ১৫৭,১৬৩, ১৬৭,১৭৩, ১৭৯,১৮১, ১৯১,১৯৩, ১৯৭,১৯৯।
৩। ১১
ও ১৩ একটি যমজ মৌলিক সংখ্যা। এরকম ৫টি যমজ মৌলিক
সংখ্যাগুলি লিখি।
সমাধানঃ
(১) ৩ ও ৫
(২) ৫ ও ৭
(৩) ১৭ ও ১৯
(৪) ২৯ ও ৩১
(৫) ৪১ ও ৪৩
৪. পরস্পর মৌলিক সংখ্যাকে রঙিন করি।
|
৮ ও ৭
|
২০ ও ৪৫
|
১৬ ও ২৫
|
|
১৫ ও ১৮
|
১৩ ও ১৫
|
১২ ও ১৪
|
সমাধানঃ
|
৮ ও ৭
|
২০ ও ৪৫
|
১৬ ও ২৫
|
|
১৫ ও ১৮
|
১৩ ও ১৫
|
১২ ও ১৪
|
কারনঃ ৮ ও ৭ এবং ১৩ ও ১৫ এর সাধারণ গুণনীয়ক ১।
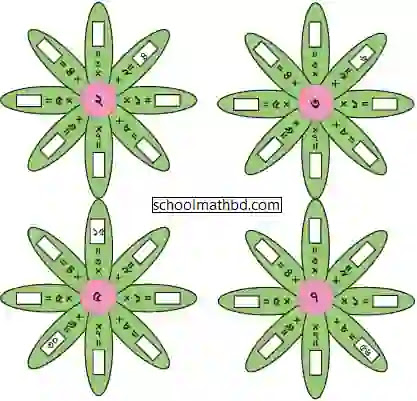
ফুলের পাপড়িতে লিখি [পাতা-১৯৬]
সমাধানঃ
আমরা সমাধানগুলো নিন্মে গাণিতিক বাক্যে দিলাম, তোমরা এটা
ফুলের পাপড়িতে লিখবে।
২×২=৪
২×১=২
২×৮=১৬
২×৭=১৪
২×৬=১২
২×৫=১০
২×৪=৮
২×৩=৬
আবার,
৩×২=৬
৩×১=৩
৩×৮=২৪
৩×৭=২১
৩×৬=১৮
৩×৫=১৫
৩×৪=১২
৩×৩=৯
আবার,
৫×২=১০
৫×১=৫
৫×৮=৪০
৫×৭=৩৫
৫×৬=৩০
৫×৫=২৫
৫×৪=২০
৫×৩=১৫
আবার,
৪×২=১৪
৪×১=৭
৪×৮=৫৬
৭×৭=৪৯
৭×৬=৪২
৭×৫=৩৫
৭×৪=২৮
৭×৩=২১
দেখছি, ৪=২×২, ৬=২×৩, ১৫=৫×৩, ৫৬=৭×৮
৪ কে দুটি ২-এর গুণফলের আকারে প্রকাশ করেছি। এখানে, ২ হলো
৪-এর গুণনীয়ক বা উৎপাদক। ৬-কে ২ ও ৩-এর গুণফলের আকারে প্রকাশ করেছি। এখানে ২ ও ৩ হলো
৬-এর গুণনীয়ক বা উৎপাদক। এখানে প্রত্যেক সংখ্যাকে তাদের গুণনীয়ক বা উৎপাদকের গুণফল
আকারে প্রকাশ করা যায়। এভাবে প্রকাশ করাকে কী বলব?
একে উৎপাদকে বিশ্নেষণ বলা হয়।
৩০-কে উৎপাদকে বিশ্লেষণ কর। কী কী ভাবে করতে পার দেখাও। [পাতা-১৯৭]
সমাধানঃ
৩০=৫×৬ আবার, ৩০=২×৩×৫ আবার, ৩০=৩×১০
অর্থাৎ আমরা ৩০ কে উপরের ৩ ভাবে উৎপাদকে বিশ্নেষণ করতে
পারি।
কিন্তু লক্ষ্য করি,
৩০=৩×১০
বা, ৩০=৩×২×৫
আবার,
৩০=৫×৬
বা, ৩০=৫×২×৩
অর্থাৎ, সর্বশেষে পাওয়া ৩০=২×৩×৫-এ ২,৩,৫ মৌলিক সংখ্যা।
সেইহেতু ৩০=২×৩×৫-একে মৌলিক উৎপাদকে বিশ্লেষণ বলে।
আবার,
৩০=১×২×৩×৫ হয়, তবে ১,২,৩,৫-এই উৎপাদকগুলিকে মৌলিক উৎপাদক
বলব না কারণ ১-কে মৌলিক সংখ্যা নয়।
৮ ও ১২-কে মৌলিক উৎপাদকে বিশ্লেষণ করি [পাতা-১৯৭]
সমাধানঃ
২|৪
২
৮=২×২×২
৮-এর মৌলিক উৎপাদকঃ ২
আবার,
২|৬
৩
১২=২×২×৩
১২-এর মৌলিক উৎপাদকঃ ২ ও ৩
মৌলিক উৎপাদকে বিশ্লেষণ করি [পাতা-১৯৭]
১৪=____×____, ১৮=+____×____×____, ২৫=____×____
সমাধানঃ
১৪=_২_×_৭_, ১৮=+_৩_×_৩_×_২_, ২৫=_৫_×_৫_
বাজারে নারকেল নিয়ে যাই [পাতা-১৯৮]
সতীশবাবু বাজারে নারকেল নিয়ে যাবেন। তিনি বস্তায় নারকেল
ভরতি করছেন। ১টি বস্তায় রেখেছেন ২৫টি নারকেল। ১৫টি বস্তায় তিনি কতগুলো নারকেল রেখেছেন
সহজে হিসাব করার চেষ্টা করি।
সমাধানঃ
১৫টি বস্তায় রেখেছেন ২৫×১৫টি নারকেল।
এখন, ১৫=৩×৫
তাই, ২৫-কে প্রথমে ৩ দিয়ে গুণ করি-
২৫×৩=৭৫
এখন, ৭৫-কে ৫ দিয়ে গুণ করি-
৭৫×৫=৩৭৫
তাহলে, ২৫×১৫=৩৭৫
অর্থাৎ তিনি ১৫টি বস্তায় রেখেছেন ৩৭৫টি নারকেল।
আবার, শ্যামলবাবু প্রতি বস্তায় ১৫টি করে ৩৫ বস্তা নারকেল
নিয়ে বাজারে গিয়েছেন। তিনি মোট কতগুলো নারকেল নিয়ে বাজারে গিয়েছেন হিসাব করি।
সমাধানঃ
১টি বস্তায় নারকেল আছে ২৫টি
৩৫টি বস্তায় নারকেল আছে ২৫× ৩৫টি
=২৫×৫×৭টি
=১২৫×৭টি
=৮৭৫টি
সাইকেল কেনার টাকা জমাই [পাতা-১৯৯]
পার্থ একটি সাইকেল কেনার জন্য ১ জানুয়ারি থেকে ৩১ জানুয়ারি
পর্যন্ত প্রতিদিন ১২ টাকা করে জমিয়েছে। সে মোট কত টাকা জমিয়েছে হিসাব করি।
সমাধানঃ
১ জানুয়ারি থেকে ৩১ জানুয়ারি = ৩১ দিন।
তাহলে, সে ৩১ দিনে জমিয়েছে ৩১×১২ টাকা
=৩১×২×২×৩
টাকা
=৬২×২×৩
টাকা
=১২৪×৩
টাকা
=৩৭২
টাকা
(১) সহজে উৎপাদকে বিশ্লেষণ করে গুণ করার করি [পাতা-১৯৯]
(ক) ৪৪×১৫
(খ)
১২৩×১২
(গ) ১০৫×১৮
(ঘ) ৯৮×২৫
(ঙ) ২১৩×২১
(চ) ২৩৭×২৭
সমাধানঃ
(ক) ৪৪×১৫
=৪৪×৩×৫
=১৩২×৫
=৬৬০
(খ)
১২৩×১২
=১২৩×২×২×৩
=২৪৬×২×৩
=৪৯২×৩
=১৪৭৬
(গ) ১০৫×১৮
=১০৫×২×৩×৩
=২১০×৩×৩
=৬৩০×৩
=১৮৯০
(ঘ) ৯৮×২৫
=৯৮×৫×৫
=৪৯০×৫
=২৪৫০
(ঙ) ২১৩×২১
=২১৩×৩×৭
=৬৩৯×৭
=৪৪৭৩
(চ) ২৩৭×২৭
=২৩৭×৩×৩×৩
=৭১১×৩×৩
=২১৩৩×৩
=৬৩৯৯
(২) ১৩৫×২৪ হিসাব করি।
সমাধানঃ
১৩৫×২৪
=১৩৫×২×২×২×৩
=২৭০×২×২×৩
=৫৪০×২×৩
=১০৮০×৩
=৩২৪০
সহজে ভাগ করি [পাতা-২০০]
উষার কাছে অনেকগুলো দেশলাই কাঠি আছে। আজ সে ঠিক করেছে সেই
দেশলাই কাঠিগুলো সমান ভাগে ভাগ করে দেশলাই বাক্সে রাখবে। উষা গুনে দেখল তার কাছে ১০৮টি
দেশলাই আছে ও ৬টি দেশলাই বাক্স আছে। আমি কি সমান সংখ্যায় ভাগ করে রাখতে পারব? নতুনভাবে
সহজে ভাগ করার চেষ্টা করি।
সমাধানঃ
৬=২×৩
১০৮÷২=৫৪
৫৪÷৩=১৮
∵ প্রতি
বাক্সে ১৮টি করে দেশলাই কাঠি রাখলাম।
সমাধানঃ
৩৬=২×২×৩×৩
২৫২÷২=১২৬
১২৬÷২=৬৩
৬৩÷৩=২১
২১÷৩=৭
অন্যভাবে,
২|১২৬
৩|৬৩
৩|২১
৭
তাই আমাদের মোট বাস দরকার ৭টি।
সমতুল্য প্রশ্নঃ আমরা বন্ধুরা ও আমাদের পরিবারের লোকজন
মিলে মোট ২৫২ জন দার্জিলিং বেড়াতে গেলাম। আমরা বাসে করে প্রতি বাসে ৩৬ জন গেলাম। তাহলে
আমাদের মোট কতটি বাস ভাড়া করতে হয়েছিল।
সমাধানঃ
২৫= ৫×৫
এখন,
৫১৭৫÷৫=১০৩৫
১০৩৫÷৫=২০৭
অথবা,
৫|১০৩৫
২০৭
∵প্রতিটি সারিতে আমগাছ আছে ২০৭টি করে।
সমতুল্য প্রশ্নঃ বাবা আমাদের একটি জমিতে ৫১৭৫টি আমের চাড়া
রোপন করলেন যেখানে প্রতিটি সারিতে তিনি সমান সংখ্যায় চারা রোপন করেছেন। আমি গুনে দেখলাম
সেখানে মোট ২৫টি সারি আছে। তাহলে এখন হিসাব করি মোট কতটি সারিতে বাবা আমের চারা রোপন
করেছেন।
সমাধানঃ
৩২=২×২×২×২×২
এখন,
৪০৬৪÷২=২০৩২
২০৩২÷২=১০১৬
১০১৬÷২=৫০৮
৫০৮÷২=২৫৪
২৫৪÷২=১২৭
∵ সমীরবাবু
১২৭টি পান
পাতার গোছ তৈরি করবেন।
সমাধানঃ
৩ সপ্তাহ =(৩×৭) দিন =২১ দিন
২১=৩×৭
৪৫১৫÷৩=১৫০৫
১৫০৫÷৭=২১৫
∵ তিনি ১ দিনে কাগজ বিলি করেছেন ২১৫টি।
সমতুল্য প্রশ্নঃ রহিমচাচা গত ২১ দিনে ৪৫১৫টি খবরের কাগজ
তার দোকান থেকে বিক্রি করলেন। তিনি প্রতিদিন কতগুলো কাগজ বিক্রি করলেন।
৫। মৌলিক উৎপাদকে বিশ্লেষণ করে ভাগ করি [পাতা-২০১]
(ক) ২৭৭২÷১৪
সমাধানঃ
১৪=২×৭
তাহলে,
২৭৭২÷২=১৩৮৬
১৩৮৬÷৭= ১৯৮
∵ ভাগফল=১৯৮
(খ) ৪৮০৬÷১৮
সমাধানঃ
১৮=২×৩×৩
এখন,
৪৮০৬÷২=২৪০৩
২৪০৩÷৩=৮০১
৮০১÷৩=২৬৭
∵ভাগফল=২৬৭
(গ) ৭৯৩৮÷৮১
সমাধানঃ
৮১=৩×৩×৩×৩
এখন,
৭৯৩৮÷৩=২৬৪৬
২৬৪৬÷৩=৮৮২
৮৮২÷৩=২৯৪
২৯৪÷৩= ৯৮
∵ভাগফল= ৯৮
(ঘ) ৫৪৮১÷৬৩
সমাধানঃ
৬৩=৭×৩×৩
এখন,
৫৪৮১÷৭=৭৮৩
৭৮৩÷৩=২৬১
২৬১÷৩=৮৭
∵ভাগফল=৮৭
(ঙ) ৫৮৮৮÷৬৪
সমাধানঃ
৬৪=৮×২×২×২
এখন,
৫৮৮৮÷৮=৭৩৬
৭৩৬÷২=৩৬৮
৩৬৮÷২=১৮৪
১৮৪÷২=৯২
∵ভাগফল=৯২
(চ) ৮৮৭৬÷২৮
সমাধানঃ
২৮=৪×৭
এখন,
৮৮৭৬÷৪=২২১৯
২২১৯÷৭=৩১৭
∵ভাগফল=৩১৭
৬। গল্প তৈরি করি, অতঃপর মৌলিক উৎপাদকে বিশ্লেষণের সাহায্যে ভাগফল নির্ণয় করিঃ
(ক) ১৩৩০÷৩৫
গল্পঃ আমাদের শ্রেণির ৩৫ জন শিক্ষার্থী মিলে বন্যার্তদের
জন্য ১৩৩০ টাকা চাঁদা দিয়েছে। সবাই সমান হারে চাঁদা দিলে প্রত্যেকে কত টাকা দিয়েছে
তা মৌলিক উৎপাদকের সাহায্যে হিসাব করে বের করি।
সমাধানঃ
৩৫=৫×৭
এখন,
১৩৩০÷৫=২৬৬
২৬৬÷৭=৩৮
∵ প্রত্যেকে
চাঁদা দিয়েছে ৩৮ টাকা।
(খ) ১৭৫৫÷২৭
গল্পঃ আবুল চাচা ২৭ টাকা কেজি দরে মোট ১৭৫৫ টাকার আম বিক্রি
করলেন। তাহলে বলো তো তিনি প্রতি কেজি আম কত দরে বিক্রি করলেন।
সমাধানঃ
২৭=৩×৩×৩
১৭৫৫÷৩=৫৮৫
৫৮৫÷৩=১৯৫
১৯৫÷৩=৬৫
∵ প্রতি
কেজি আম বিক্রি করলেন ৬৫ টাকা করে।
(গ) ১৫৬০÷৩০
গল্পঃ মিতু প্রতিদিন তার স্কুলে যাতায়াত বাবদ যে টাকা খরচ
করে তার হিসাবে দেখা গেল তার মাসিক খরচ ১৫৬০ টাকা। তাহলে তার দৈনিক যাতাযাত খরচ কত?
সমাধানঃ
১ মাস = ৩০ দিন
৩০=৫×২×৩
এখন,
১৫৬০÷৫=৩১২
৩১২÷২=১৫৬
১৫৬÷৩=৫২
∵ মিতুর
দৈনিক যাতায়াত খরচ ৫২ টাকা
(ঘ) ২০৫৮÷৪৯
গল্পঃ শ্রীমান রায় প্রতি জোড়া নারকেল ৪৯ টাকা দরে বিক্রি
করে ২০৫৮ টাকা পেলেন। তাহলে তিনি মোট কত জোড়া নারকেল বিক্রি করলেন।
সমাধানঃ
৪৯=৭×৭
এখন,
২০৫৮÷৭=২৯৪
২৯৪÷৭=৪২
অর্থাৎ তিনি ৪২ জোড়া নারকেল বেঁচলেন।
পরের পাঠঃ
আকার তৈরি করি