SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-২.২ সেট ও ফাংশনঃ ডোমেন-রেঞ্জ

Admin

07 February

সেট ও ফাংশনঃ ডোমেন-রেঞ্জ

১. 8 এর গুণনীয়ক সেট কোনটি?

(ক) {8,16,24,…} (খ) {1,2,4,8}
(গ) {2,4,8} (ঘ) {1,2}
উত্তরঃ খ

২. সেট C হতে সেট B এ একটি সম্পর্ক R হলে নিচের কোনটি সঠিক?

(ক) R⊂C (খ) R⊂B
(গ) R⊆C✕B (ঘ) C✕B⊆R
উত্তরঃ গ

৩. A={1,2}, B={2,5} হলে, P(A∩B)এর সদস্য সংখ্যা নিচের কোনটি?

(ক) 1 (খ) 2
(গ) 3 (ঘ) 8
উত্তরঃ খ

৪. নিচের কোনটি {x∈N:13<x<17 এবং x মৌলিক সংখ্যা} সেটটিকে তালিকা পদ্ধতিতে প্রকাশ করে?

(ক) ∅ (খ) {0}
(গ) {∅ } (ঘ) {13,17}
উত্তরঃ ক

৫. A∪B={a,b,c} হলে,

(i).. A={a,b}, B={a,b,c}
(ii).. A={a,b,c}, B={b,c}
(iii).. A={a,b}, B={c}

উপর্যুক্ত তথ্যের আলোকে নিচের কোনটি সঠিক?
(ক) i (খ) ii
(গ) i ও ii (ঘ) i, ii ও iii
উত্তরঃ ঘ

৬. A ও B দুইটি সসীম সেটের জন্য

(i).. A✕B={(x,y):x∈N এবং y∈B}
(ii).. n(A)=a,n(B)=b হলে, n(A✕B)=ab
(iii).. A✕B এর প্রতিটি সদস্য একটি ক্রমজোড়।

উপর্যুক্ত তথ্যের আলোকে নিচের কোনটি সঠিক?
(ক) i ও ii (খ) i ও iii
(গ) ii ও iii (ঘ) i, ii ও iii
উত্তরঃ ঘ

A={6,7,8,9,10,11,12,13} হলে, নিচের ৭-৯ প্রশ্নগুলোর উত্তর দাওঃ

৭. A সেটের সঠিক প্রকাশ কোনটি?

(ক) { x∈N:6<x<13} (খ) { x∈N:6≤x<13}
(গ) {x∈N:6≤x≤13} (ঘ) { x∈N :6<x≤13}
উত্তরঃ গ

৮. A সেটের মৌলিক সংখ্যাগুলোর সেট কোনটি?

(ক) {6,8,10,12} (খ) {7,9,11,13}
(গ) {7,11,13} (ঘ) {9,12}
উত্তরঃ গ

৯. A সেটের 3 এর গুণিতকগুলোর সেট কোনটি?

(ক) {6,9} (খ) {6,11}
(গ) {9,12} (ঘ) {6,9,12}
উত্তরঃ ঘ

১০. যদি A={3,4}, B={2,4}, x∈A এবং y∈B হয়, তবে A ও B এর উপাদানগুলোর মধ্যে x>y সম্পর্ক বিবেচনা করে অন্বয়টি নির্ণয় কর।

সমাধানঃ

দেওয়া আছে, A={3,4}, B={2,4}, x∈A এবং y∈B
প্রশ্নমতে, অন্বয় R={(x,y):x∈A, y∈B এবং x>y}
এখন,
A✕B={3,4}✕{2,4}
={(3,2),(3,4),(4,2),(4,4)}
∴R={(3,2),(4,2)}
∴নির্ণেয় অন্বয়={(3,2),(4,2)}

১১. যদি C={2,5}, D={4,6,7}, x∈C এবং y∈D হয়, তবে C ও D এর উপাদানগুলোর মধ্যে x+1<y সম্পপর্ক বিবেচনা করে অন্বয়টি নির্ণয় কর।

সমাধানঃ

দেওয়া আছে, C={2,5}, D={4,6,7}, x∈C এবং y∈D
প্রশ্নমতে, অন্বয় R={(x,y):x∈C, y∈D এবং x+1<y}
এখন,
C✕D={2,5}✕{4,6}
={(2,4),(2,6),(5,4),(5,6)}
∴R={(2,4),(2,6)}
∴নির্ণেয় অন্বয়={(2,4),(2,6)}

১২. f(x)=x⁴+5x-3 হলে, f(-1), f(2) এবং f(1/2) এর মান নির্ণয় কর।

সমাধানঃ

দেওয়া আছে, f(x)=x⁴+5x-3
∴f(-1)= (-1)⁴+5✕(-1)-3=1-5-3=-7;
(f(2)= 2⁴+5✕2-3=16+10-3=23
এবং, f(1/2)= (1/2)⁴+5✕(1/2)-3=1/16+5/2-3=(1+40-48)/16=-7/16

১৩. যদি f(y)=y³+ky²-4y-8 হয়, তবে k এর কোন মানের জন্য f(-2)=0 হবে?

সমাধানঃ

দেওয়া আছে, f(y)=y³+ky²-4y-8
∴f(-2)= (-2)³+k(-2)²-4✕(-2)-8=-8+4k+8-8=-8+4k
প্রশ্নমতে, f(-2)=0 হবে
তাহলে, -8+4k=0
বা, -8=-4k
বা, 4k=8
বা, k=8/4
বা, k=2
∴k এর নির্ণেয় মান 2

১৪. f(x)=x³-6x²+11x-6 হয়, তবে x এর কোন মানের জন্য f(x)=0 হবে?

সমাধানঃ

দেওয়া আছে, f(x)=x³-6x²+11x-6
প্রশ্নমতে, f(x)=0 হবে
তাহলে, x³-6x²+11x-6=0
বা, x³-x²-5x²+5x+6x-6=0
বা, x²(x-1)-5x(x-1)+6(x-1)=0
বা, (x²-5x+6)(x-1)=0
বা, (x-1){x²-3x-2x+6)}=0
বা, (x-1){x(x-3)-2(x-3)}=0
বা, (x-1)(x-3)(x-2)=0
বা, x-1=0; x-3=0; x-2=0
বা, x=1, x=3, x=2
∴x এর নির্ণেয় মান 1,2 বা 3.

১৫. যদি f(x)=(2x+1)/(2x-1) হয়, তবে {f(1/x²)+1}/{f(1/x²)-1} এর মান নির্ণয় কর।

সমাধানঃ
দেওয়া আছে,
f(x) =	2x+1 ------- 2x-1
∴f(1/x²) =	2.(1/x²)+1 ---------------- 2.(1/x²)-1
=	2/x²+1 ----------- 2/x²-1
=	2+x² ---------- x² ----------- 2-x² ---------- x²
=	2+x² ------ x²		✕				x² --------- 2-x²
=	2+x² ^--------- 2-x²
f(1/x²)+1=	2+x² ------------ 2-x²					+			1
=	2+x²+2-x² ---------------- 2-x²
=	4 ---------- 2-x²
f(1/x²)-1=	2+x² -------- 2-x²			-						1
=	2+x²-2+x² ------------- 2-x²
=	2x² ------------- 2-x²
∴{f(1/x²)+1}/{f(1/x²)-1}=
	4 ------ 2-x²	/						2x² --------- 2-x²
=	4 ------ 2-x²	✕			2-x² ------- 2x²
=	2 ----- x²

১৬. g(x)=(1+x²+x⁴)/x² হলে, দেখাও যে, g(1/x²)=g(x²)

সমাধানঃ
দেওয়া আছে,
g(x)	=	1+x²+x⁴ ----------- x²
∴g(1/x²)	=	1+(1/x²)²+(1/x²)⁴ ---------------- (1/x²)²
	=	1+1/x⁴+1/x⁸ ---------------- 1/x⁴
	=	x⁸+x⁴+1 ---------- x⁸ ------------ 1 ------------ x⁴
	=	(x⁸+x⁴+1)✕x⁴ ------------------ x⁸
	=	x⁸+x⁴+1 ----------- x⁴
g(x²)	=	1+(x²)²+(x²)² ----------------- (x²)²
	=	1+x⁴+x⁸ ------------ x⁴
∴g(1/x²)	=	g(x²) (দেখানো হলো)

১৭. নিচের অন্বয়গুলো থেকে ডোমেন এবং রেঞ্জ নির্ণয় কর।

ক) R={(2,1),(2,2),(2,3)}

সমাধানঃ

প্রদত্ত R অন্বয়ের ক্রম্পজোড়গুলোর প্রথম উপাদান 2 এবং ২য় উপাদানগুলো 1,2,3.
∴ডোমেন R={2}
রেঞ্জ R{1,2,3}

খ) S={(-2,-4),(-1,1)(0,0),(1,1),(2,4)}

সমাধানঃ

প্রদত্ত S অন্বয়ের ক্রম্পজোড়গুলোর প্রথম উপাদান -2,-1,0,1,2 এবং ২য় উপাদানগুলো 0,1,4.
∴ডোমেন R={-2,-1,0,1,2}
রেঞ্জ R{0,1,4}

গ) F={(1/2,0),(1,1),(1,-1),(5/2,2),(5/2,-2)}

সমাধানঃ

প্রদত্ত F অন্বয়ের ক্রম্পজোড়গুলোর প্রথম উপাদান 1/2,1,5/2 এবং ২য় উপাদানগুলো -2,-1,0,1,2.
∴ডোমেন R={1/2,1,5/2}
রেঞ্জ R{-2,-1,0,1,2}

১৮. নিচের অন্বয়গুলোকে তালিকা পদ্ধতিতে প্রকাশ কর এবং ডোমেন ও রেঞ্জ নির্ণয় কর।

ক) R={(x,y):x∈A,y∈A এবং x+y=1} যেখানে A={-2,-1,0,1,2}

সমাধানঃ

দেওয়া আছে, R={(x,y):x∈A,y∈A এবং x+y=1}, A={-2,-1,0,1,2}
প্রদত্ত শর্ত হতে, x+y=1 বা, y=1-x
এখন, x∈A এর জন্য, y=1-x এর মান নির্ণয় করিঃ

x	-2	-1	0	1	2
y	3	2	1	0	-1

∴যেহেতু, 3∉A সেহেতু, (-2,3) ∉R.
R={(-1,2),(0,1),(1,0),(2,-1)}
∴ডোমেন R={-1,0,1,2}
রেঞ্জ R={-1,0,1,2}

খ) F={(x,y):x∈C,y∈C এবং y=2x} যেখানে C={-1,0,1,2,3}

সমাধানঃ

দেওয়া আছে, F={(x,y):x∈C,y∈C এবং y=2x}, C={-1,0,1,2,3}
প্রদত্ত শর্ত হতে, y=2x
এখন, x∈C এর জন্য, y=2x এর মান নির্ণয় করিঃ

x	-1	0	1	2	3
y	-2	0	2	4	6

∴যেহেতু, -2,4,6∉C সেহেতু, (-1,-2),(2,4),(3,6) ∉F.
F={(0,0),(1,2)}
∴ডোমেন F={0,1}
রেঞ্জ F={0,2}

১৯. ছক কাগজে (-3,2), (0,-5), (1/2, -5/6) বিন্দুগুলো স্থাপন কর।

সমাধানঃ

মনে করি, XOX’ ও YOY’ যথাক্রমে x অক্ষ ও y অক্ষ। o মূলবিন্দু। ছক কাগজের উভয় অক্ষের ক্ষুদ্রতম বর্গের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি।
(-3,2) বিন্দুর ভুজ =-3 এবং কোটি=2। কাজেই x অক্ষের দিকে বামে -3 একক গিয়ে y অক্ষের ওপরের দিকে 2 একক যাওয়ার পর যে বিন্দুটি পাওয়া যাবে সেটিই হবে (-3,2) বিন্দুর অবস্থান।
অনুরুপভাবে, (0,-5), (1/2, -5/6) বিন্দুগুলো ছক কাগজে স্থাপন করি।
(0,-5) y O OY’ 5 (0,-5)
(1/2,-5/6) O OX OY’ (1/2,-5/6)

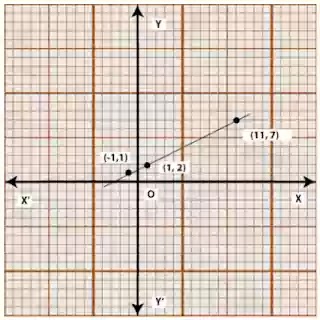
২০. ছক কাগজে (1,2), (-1,1), (11,7) বিন্দু তিনটি স্থাপন করে দেখাও যে, বিন্দু তিনটি একই সরলরেখায় অবস্থিত।

সমাধানঃ

মনে করি, XOX’ ও YOY’ যথাক্রমে x অক্ষ ও y অক্ষ। o মূলবিন্দু। ছক কাগজে উভয় অক্ষের ক্ষুদ্রতম বর্গের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি এবং (1,2), (-1,1), (11,7) বিন্দুগুলো স্থাপন করি। বিন্দু তিনটি যোগ করে একটি সরলরেখা পেলাম। অর্থাৎ, বিন্দু তিনটি একই সরলরেখায় অবস্থিত (দেখানো হলো)।

২১. সার্বিক সেট U={x:x∈N এবং x বিজোড় সংখ্যা}

A={x:x∈N এবং 2≤x≤7}
B={x:x∈N এবং 3<x<6}
C={x:x∈N এবং x²>5 এবং x³<130}

ক) A সেটকে তালিকা পদ্ধতিতে প্রকাশ কর।

সমাধানঃ

দেওয়া আছে, U={x:x∈N এবং x বিজোড় সংখ্যা}; A={x:x∈N এবং 2≤x≤7}
আমরা জানি, স্বাভাবিক সংখ্যার সেট N={1,2,3,4,5……..}
∴ তাহলে, 2 হেকে 7 পর্যন্ত বিজোর সংখ্যাসমূহ 3,5,7
A={3,5,7}

গ) B✕C এবং P(A∩C) নির্ণয় কর।

সমাধানঃ

ক, খ হতে,
A={3,5,7}
B={5}
C={3,5}
এখন,
A∩C={3,5,7}∩{3,5}={3,5}
∴P(A∩C)={{3,5},{3},{5},∅}
∴B✕C={5}✕{3,5}={(5,3),(5,5)}

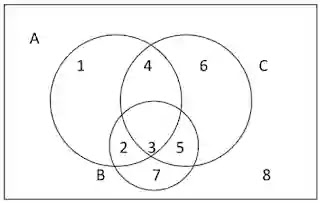
২২. ভেনচিত্রটি লক্ষ করিঃ

ক) B সেটকে গঠন পদ্ধতিতে প্রকাশ কর।

সমাধানঃ

ভেনচিত্র হতে, B সেটের উপাদানগুলোঃ 2,3,5,7 যা মৌলিক সংখ্যা।
∴নির্ণেয় সেট, B=A={x:x∈N এবং 2≤x≤7}

খ) উদ্দীপক ব্যবহার করে A∪(B∩C)=(A∪B)∩(A∪C) সম্পর্কটির সত্যতা যাচাই কর।

সমাধানঃ

ভেনচিত্রের উদ্দীপদ হতে,
A={1,2,3,4}, B={2,3,5,7}, C={3,4,5,6}
∴B∩C={2,3,5,7}∩{3,4,5,6}={3,5}
বামপক্ষ=A∪(B∩C)= {1,2,3,4}∪{3,5}={1,2,3,4,5}
আবার,
A∪B={1,2,3,4}∪{2,3,5,7}={1,2,3,4,5,7}
A∪C={1,2,3,4}∪{3,4,5,6}={1,2,3,5,6}
∴ ডানপক্ষ=(A∪B)∩(A∪C)= {1,2,3,4,5,7}∩{1,2,3,5,6}={1,2,3,4,5}
∴ বামপক্ষ=ডানপক্ষ (সত্যতা যাচাই হলো)

গ) S=(B∪C)^C✕A হলে, ডোম S নির্ণয় কর।

সমাধানঃ

দেওয়া আছে,
U={1,2,3,4,5,6,7,8}
A={1,2,3,4}, B={2,3,5,7}, C={3,4,5,6}
এখন, BUC={2,3,5,7}U{3,4,5,6}={2,3,4,5,6,7}
∴ (B∪C)^C=U-(B∪C)={1,2,3,4,5,6,7,8}-{2,3,4,5,6,7}={1,8}
∴S=(B∪C)^C✕A={1,8}✕{1,2,3,4}={1,1),(1,2),(1,3),(1,4),(8,1),(8,2),(8,3),(8,4)}
S অন্বয়ের ক্রমজোড়গুলোর প্রথম উপাদান 1,8
∴ডোম S={1,8}

২৩. y=f(x)=(4x-7)/(2x-4) একটি ফাংশন

ক) f(-1/2) এর মান নির্ণয় কর।

সমাধানঃ
দেওয়া আছে,	f(x)	=	4x-7 2x-4
	∴f(-1/2)	=	4✕(-1/2)-7 2✕(-1/2)-4
		=	-4/2-7 -2/2-4
		=	-2-7 -1-4
		=	-9 -5
		=	9 5

খ) {f(x)+2}/{f(x)-1} এর মান নির্ণয় কর।

সমাধানঃ
দেওয়া আছে,
		y	=	f(x)	=	4x-7 2x-4
	∴	f(x)+2		=	4x-7 2x-4		+	2
				=	4x-7+4x-8 2x-4
				=	8x-15 2x-4
		f(x)-1		=	4x-7 2x-4		-	1
				=	4x-7-2x+4 2x-4
				=	2x-4 2x-3
∴		f(x)+2 f(x)-1		=	8x-15 2x-4 2x-4 2x-3
				=	8x-15 2x-4		X	2x-4 2x-3
					8x-15 2x-3

গ) দেখাও যে, f(y)=x

সমাধানঃ
দেওয়া আছে,
	y=	f(x)=	4x-7 2x-4
	∴	f(y)=	4y-7 2y-4
এখন,	y=	4x-7 2x-4
	বা, 2xy-4y=4x-7
	বা, 2xy-4x=4y-7
	বা, x(2y-4)=4y-7
	বা, x=	4y-7 2y-7
	বা, x=	f(y)	(দেখানো হলো)

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।